
数列{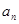 }中,a1=3,
}中,a1=3,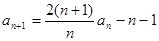 ,
,
(1)求a1、a2、a3、a4;
(2)用合情推理猜测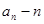 关于n的表达式(不用证明);
关于n的表达式(不用证明);
(3)用合情推理猜测{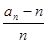 }是什么类型的数列并证明;
}是什么类型的数列并证明;
(4)求{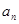 }的前n项的和。
}的前n项的和。
(1)3,10,27,68
(2) an-n=n 2n
2n
(3) =2
=2 2n-1,
2n-1,
解析试题分析:解:(1) a1=3, a2= a1-1-1=10,a3=
a1-1-1=10,a3= a2-2-1=27,
a2-2-1=27,
a4=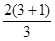 a3-3-1=68 2分
a3-3-1=68 2分
(2)由(1),a1-1=2=1 2,a2-2=8=2
2,a2-2=8=2 22,a3-3=24=3
22,a3-3=24=3 23,a4-4=64=4
23,a4-4=64=4 24,
24,
猜测an-n=n 2n, 4分
2n, 4分
(3) 由(2),an-n=n 2n,
2n, =
= 2n,因此可推测{
2n,因此可推测{ }是等比数列 5分证明如下:
}是等比数列 5分证明如下: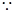 an+1=
an+1= an-n-1,
an-n-1, an+1-(n+1)=
an+1-(n+1)=  an-2(n+1)=2(n+1)(
an-2(n+1)=2(n+1)( -1),
-1),
 =2
=2
 , 而
, 而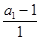 =2
=2 0,
0,  {
{ }是首项为2,公比为2的等比
}是首项为2,公比为2的等比
数列; 8分
(4)由(3) =2
=2 2n-1,
2n-1, an="n+" n 2n, 10分
an="n+" n 2n, 10分
{an}的前n项的和: Sn= +1
+1 2+2
2+2 22+3
22+3 23+ +n
23+ +n 2n。
2n。
记P=1 2+2
2+2 22+3
22+3 23+ +n
23+ +n 2n,则2P-P= n
2n,则2P-P= n 2n+1-(2+22+23+ +2n)= (n-1)
2n+1-(2+22+23+ +2n)= (n-1) 2n+1+2
2n+1+2 P=(n-1)
P=(n-1) 2n+1+2,
2n+1+2,  Sn=
Sn= +(n-1)
+(n-1) 2n+1+2. 13分
2n+1+2. 13分
考点:合情推理
点评:解决的关键是能根据递推关系来归纳猜想来得到数列的通项公式的特点,进而分析证明,属于基础题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
下图是一个按照某种规律排列出来的三角形数阵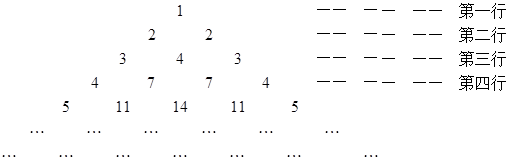
假设第 行的第二个数为
行的第二个数为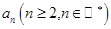
(1)依次写出第七行的所有7个数字(不必说明理由);
(2)写出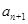 与
与 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出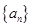 的通项公式
的通项公式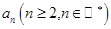 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线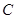 :
: ,数列
,数列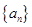 的首项
的首项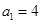 ,且
,且
当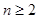 时,点
时,点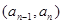 恒在曲线
恒在曲线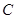 上,数列{
上,数列{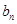 }满足
}满足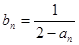
(1)试判断数列 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列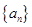 和
和 的通项公式;
的通项公式;
(3)设数列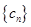 满足
满足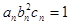 ,试比较数列
,试比较数列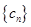 的前
的前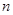 项和
项和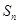 与
与 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
对数列{an},规定{△an}为数列{an}的一阶差分数列,其中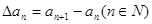 。
。
对自然数k,规定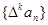 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中 。
。
(1)已知数列{an}的通项公式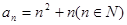 ,试判断
,试判断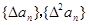 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列{an}首项a1=1,且满足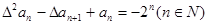 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
(3)对(2)中数列{an},是否存在等差数列{bn},使得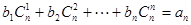 对一切自然
对一切自然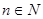 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数列{an}满足4a1=1,an-1=[(-1)nan-1-2]an(n≥2),(1)试判断数列{1/an+(-1)n}是否为等比数列,并证明;(2)设an2?bn=1,求数列{bn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com