
分析 (Ⅰ)由题意知f(0)=g(0),从而解得;
(Ⅱ)令h(x)=f(x)+g(x)=|x-1|+x2+2x+1=x2+3x=(x+$\frac{3}{2}$)2-$\frac{9}{4}$,从而求最值.
解答 解:(Ⅰ)函数f(x)和g(x)的图象与y轴相交于同一点,
f(0)=g(0),
解得a=1.
(Ⅱ)令h(x)=f(x)+g(x)
=|x-1|+x2+2x+1,
∵x∈[1,2],
∴h(x)=f(x)+g(x)
=x-1+x2+2x+1
=x2+3x=(x+$\frac{3}{2}$)2-$\frac{9}{4}$,
h(x)的对称轴为x=-$\frac{3}{2}$,
当x∈[1,2]时,h(x)单调递增,
故hmin(x)=h(1)=4,hmax(x)=h(2)=10.
点评 本题考查了学生的化简运算能力及二次函数的性质应用.


科目:高中数学 来源: 题型:选择题
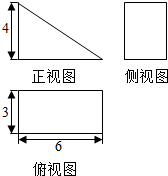
| A. | 36 | B. | $54+6\sqrt{13}$ | C. | $54+12\sqrt{5}$ | D. | $30+6\sqrt{73}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 25 | C. | $\sqrt{41}$ | D. | $5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{8}{3}c{m^3}$ | B. | $\frac{4}{3}c{m^3}$ | C. | $\frac{2}{3}c{m^3}$ | D. | $\frac{1}{3}c{m^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
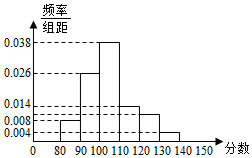 某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)
某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com