
分析 利用基本不等式的性质即可得出.
解答 解:∵2a+b=1,a>0,b>0,
∴2$\sqrt{ab}$-4a2-b2=$\sqrt{2}$•$\sqrt{2ab}$-[(2a)2+b2]≤$\sqrt{2}$•$\frac{2a+b}{2}$-$\frac{(2a+b)^{2}}{2}$=$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$=$\frac{\sqrt{2}-1}{2}$,
当且仅当a=$\frac{1}{4}$,b=$\frac{1}{2}$时,等号成立,
故答案为:$\frac{\sqrt{2}-1}{2}$.
点评 本题考查了基本不等式及其变形应用,属于基础题.


科目:高中数学 来源: 题型:解答题
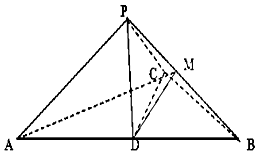 如图,在三棱锥P-ABC中,∠ACB=90°,CB=4,AB=12,D为
如图,在三棱锥P-ABC中,∠ACB=90°,CB=4,AB=12,D为查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
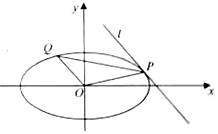 如图,P(x0,y0)是椭圆$\frac{{x}^{2}}{3}$+y2=1的上的点,l是椭圆在点P处的切线,O是坐标原点,OQ∥l与椭圆的一个交点是Q,P,Q都在x轴上方
如图,P(x0,y0)是椭圆$\frac{{x}^{2}}{3}$+y2=1的上的点,l是椭圆在点P处的切线,O是坐标原点,OQ∥l与椭圆的一个交点是Q,P,Q都在x轴上方查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com