
分析 (I)由2${\;}^{{a}_{n}}$,2${\;}^{{a}_{n+1}}$,2${\;}^{{a}_{n+2}}$成等比数列,可得$({2}^{{a}_{n+1}})^{2}$=2${\;}^{{a}_{n}}$•2${\;}^{{a}_{n+2}}$,可得2an+1=an+an+2.利用等差数列的通项公式可得an.
(II)利用“错位相减法”、等差数列等比数列的求和公式即可得出.
解答 解:(I)∵2${\;}^{{a}_{n}}$,2${\;}^{{a}_{n+1}}$,2${\;}^{{a}_{n+2}}$成等比数列,∴$({2}^{{a}_{n+1}})^{2}$=2${\;}^{{a}_{n}}$•2${\;}^{{a}_{n+2}}$,∴2an+1=an+an+2.
∴数列{an}为等差数列,设公差为d,∵a3=5,a5+a6=20,
∴a1+2d=5,2a1+9d=20,
解得a1=1,d=2.
∴an=1+2(n-1)=2n-1.
(II)bn=an-(-1)nn=(2n-1)-(-1)nn.
设数列{(-1)nn}的前n项和为Sn,
则Sn=-1+2-3+…+(-1)nn.
∴-Sn=1-2+3+…+(-1)n(n-1)+(-1)n+1n,
∴2Sn=-1+1-1+…+(-1)n-(-1)n+1n=$\frac{-[1-(-1)^{n}]}{1-(-1)}$-(-1)n+1n,
∴Sn=$\frac{(-1)^{n}-1}{4}$+$\frac{(-1)^{n}n}{2}$.
∴Tn=$\frac{n(1+2n-1)}{2}$-$\frac{(-1)^{n}-1}{4}$-$\frac{(-1)^{n}n}{2}$=n2-$\frac{(-1)^{n}-1}{4}$-$\frac{(-1)^{n}n}{2}$.
∴T21=212-$\frac{-2}{4}$-$\frac{-21}{2}$=452.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
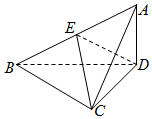 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-sin2x | B. | f(x)的图象关于x=-$\frac{π}{3}$对称 | ||
| C. | f($\frac{7π}{3}$)=$\frac{1}{2}$ | D. | f(x)的图象关于($\frac{π}{12}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.
如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{11}{16}$ | C. | $\frac{5}{8}$ | D. | $\frac{5}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
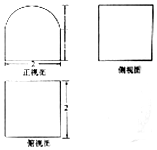 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )| A. | 12+3π | B. | 10+3π | C. | 12+4π | D. | 10+4π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com