
| 分组 | [29.86, 29.90) | [29.90,29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 15 | 30 | 125 | 198 | 77 | 35 | 20 |
| 分组 | [29.86, 29.90) | [29.90, 29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 40 | 70 | 79 | 162 | 59 | 55 | 35 |
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (1)由已知可得:2×2列联表,
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | 400 | 300 | 700 |
| 非优质品 | 100 | 200 | 300 |
| 合计 | 500 | 500 | 1000 |
解答 解:(1)由已知可得:2×2列联表,
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | 400 | 300 | 700 |
| 非优质品 | 100 | 200 | 300 |
| 合计 | 500 | 500 | 1000 |
| X | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{3}{5}$ | $\frac{3}{10}$ |
点评 本题考查了独立性检验数学及其公式、超几何分布列及其数学期望,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:解答题
已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时有
时有 .
.
①求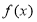 的解析式;
的解析式;
②求 的值域;
的值域;
③若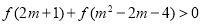 ,求
,求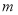 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )
如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )| A. | 重心 | B. | 垂心 | C. | 内心 | D. | 外心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com