Question

设函数f（x）=ax⁵+bx³+c的图象过点（0，1），当x=1取得极值

13

15

．
（1）求f（x）；
（2）求f（x）的单调区间和极值．

Answer 1

考点：利用导数研究函数的单调性,函数解析式的求解及常用方法,函数在某点取得极值的条件

专题：导数的综合应用

分析：（1）根据条件，建立方程关系即可求f（x）；
（2）求函数的导数，利用函数导数和函数单调性以及极值关系，即可求f（x）的单调区间和极值．

解答： 解：（1）∵函数f（x）=ax⁵+bx³+c的图象过点（0，1），
∴f（0）=c=1，即c=1，
函数的导数f′（x）=5ax⁴+3bx²，
∵当x=1取得极值

13

15

．
∴f（1）=

13

15

，且f′（1）=0．
即

a+b+1= 13 15 5a+3b=0

，解得a=

1

5

，b=-

1

3

，
则f（x）=

1

5

x⁵-

1

3

x³+1；
（2）∵f（x）=

1

5

x⁵-

1

3

x³+1；
∴f′（x）=x⁴-x²=x²（x²-1），
由f′（x）=x²（x²-1）=0，
解得x=0或x=1或x=-1，
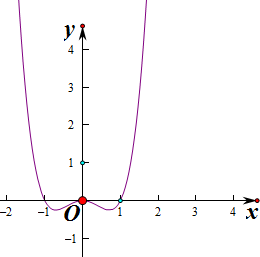
当x＜-1或x＞1时，f′（x）＞0，此时函数单调递增，
当-1＜x＜1时，f′（x）≤0，此时函数单调递减，
即函数的单调递减区间为（-1，1），单调递增区间为（-∞，-1）和（1，+∞），
且当x=-1时函数取得极大值f（-1）=

13

15

，
当x=1时函数取得极小值f（1）=

17

15

．

点评：本题主要考查函数的单调性极值和导数之间的关系，根据条件求出a，b，c的值是解决本题的关键，考查学生的运算能力．