
分析 利用等差数列、等比数列的定义和性质,分别求得${a_{k_n}}$项的通项公式,可得${k_n}=2•{3^{n-1}}-1$,再利用拆项法进行求和,可得结论.
解答 解:设{an}首项为a1,公差为d,∵a1,a5,a17成等比数列,∴a52=a1a17,
∴(a1+4d)2=a1(a1+16d),∴a1=2d.
设等比数列公比为q,则 q=$\frac{{a}_{5}}{{a}_{1}}$=$\frac{{a}_{1}+4d}{{a}_{1}}$=3,
对${a_{k_n}}$项来说,在等差数列中:${a_{k_n}}={a_1}+({k_n}-1)d=\frac{{{k_n}+1}}{2}{a_1}$,在等比数列中:${a_{k_n}}={a_1}{q^{n-1}}={a_1}{3^{n-1}}$.
∴${k_n}=2•{3^{n-1}}-1$,
∴${k_1}+{k_2}+…{k_n}=(2•{3^0}-1)+(2•{3^1}-1)+…+(2•{3^{n-1}}-1)=2(1+3+…+{3^{n-1}})-n$=3n-n-1.
点评 本题主要考查等差数列、等比数列的定义和性质的综合应用,用拆项法进行求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5,(-2,+∞) | B. | -5,(-2,+∞) | C. | 5,(-∞,2) | D. | 5,(-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
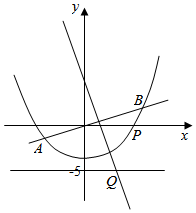 如图,直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4交于A,B两点,线段AB的垂直平分线与直线y=-5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为30.
如图,直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4交于A,B两点,线段AB的垂直平分线与直线y=-5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为30.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
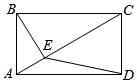
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
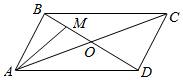 如图,在平行四边形ABCD中,AB=1,AD=2,∠BAD=60°,BD,AC相交于点O,M为BO中点.设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.
如图,在平行四边形ABCD中,AB=1,AD=2,∠BAD=60°,BD,AC相交于点O,M为BO中点.设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com