
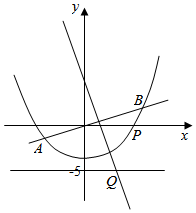
 如图,直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4交于A,B两点,线段AB的垂直平分线与直线y=-5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为30.
如图,直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4交于A,B两点,线段AB的垂直平分线与直线y=-5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为30. 分析 把直线方程抛物线方程联立求得交点A,B的坐标,则AB中点M的坐标可得,利用AB的斜率推断出AB垂直平分线的斜率,进而求得AB垂直平分线的方程,把y=-5代入求得Q的坐标;设出P的坐标,利用P到直线0Q的距离求得三角形的高,利用两点间的距离公式求得QO的长,最后利用三角形面积公式表示出三角形OPQ,利用x的范围和二次函数的单调性求得三角形面积的最大值.
解答 解:直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4联立,得到A(-4,-2),B(8,4),
从而AB的中点为M(2,1),
由kAB═$\frac{1}{2}$,直线AB的垂直平分线方程y-1=-2(x-2).
令y=-5,得x=5,
∴Q(5,-5).
∴直线OQ的方程为x+y=0,设P(x,$\frac{1}{8}$x2-4).
∵点P到直线OQ的距离d=$\frac{|x+\frac{1}{8}{x}^{2}-4|}{\sqrt{2}}$=$\frac{1}{8\sqrt{2}}$|x2+8x-32|,|OQ|=5$\sqrt{2}$,
∴S△OPQ=$\frac{1}{2}$|OQ|d=$\frac{5}{16}$|x2+8x-32|,|
∵P为抛物线上位于线段AB下方的点,且P不在直线OQ上,
∴-4≤x<4$\sqrt{3}$-4或4$\sqrt{3}$-4<x≤8.
∵函数y=x2+8x-32在区间[-4,8]上单调递增,
∴当x=8时,△OPQ的面积取到最大值30.
故答案为:30.
点评 本题主要考查了抛物线的应用,点到直线的距离公式.考查了对解析几何基础知识的灵活运用.


科目:高中数学 来源: 题型:填空题
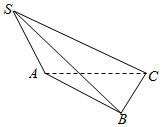 在如图所示的三棱锥S-ABC中,SA=AB=SB=$\sqrt{2}$,BC=AC=1,SC=$\sqrt{3}$,则三棱锥S-ABC的外接球的表面积为3π.
在如图所示的三棱锥S-ABC中,SA=AB=SB=$\sqrt{2}$,BC=AC=1,SC=$\sqrt{3}$,则三棱锥S-ABC的外接球的表面积为3π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com