
分析 (Ⅰ)根据函数奇偶性的定义进行求解,
(Ⅱ)根据一元二次函数单调区间和对称轴之间的关系进行求解.
(Ⅲ)根据对称轴和单调区间的关系进行讨论求解.
解答 解:(Ⅰ)∵函数f(x)在区间[-5,5]上为偶函数,
∴对称轴为y轴,即-$\frac{a}{2}$=0,则a=0;
(Ⅱ)∵函数f(x)在区间[-5,5]上为单调函数,
∴$-\frac{a}{2}≤-5$或$-\frac{a}{2}≥5$,
∴a≥10或a≤-10;
所以当a≥10或a≤-10时,函数f(x)在区间[-5,5]上为单调函数;
(Ⅲ)①若$-\frac{a}{2}≤0$,即a≥0,当x=5时,f(x)max=27+5a,
②若$-\frac{a}{2}>0$,即a<0,当x=-5时,f(x)max=27-5a.
综上所述:若a≥0,当x=5时,f(x)max=27+5a;
若a<0,当x=-5时,f(x)max=27-5a.
点评 本题主要考查一元二次函数奇偶性,单调性和最值性的应用,根据对称轴和单调区间的关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{16}{3}$+8π | B. | $\frac{32}{3}$+8π | C. | 16+8π | D. | $\frac{16}{3}$+16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,(-2,+∞) | B. | -5,(-2,+∞) | C. | 5,(-∞,2) | D. | 5,(-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{4}{3})$ | B. | $(\frac{2}{3},1]$ | C. | $[\frac{2}{3},1]$ | D. | $[1,\frac{4}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
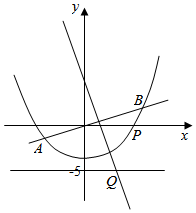 如图,直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4交于A,B两点,线段AB的垂直平分线与直线y=-5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为30.
如图,直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4交于A,B两点,线段AB的垂直平分线与直线y=-5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为30.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com