
分析 (1)设“第1次抽到黑球”为事件A,“第2次抽到黑球”为事件B,则n(A)=12,n(AB)=6,由此能求出在第1次抽到黑球的条件下,第2次抽到黑球的概率.
(2)设事件C表示“2球中至少有一个黑球”,事件D表示“2球都是黑球”,由此能求出在已知其中一个球为黑球的条件下,另一个球也是黑球的概率.
解答 解:(1):设“第1次抽到黑球”为事件A,“第2次抽到黑球”为事件B,
则n(A)=${C}_{3}^{1}{C}_{4}^{1}$=12,
n(AB)=${C}_{3}^{1}{C}_{2}^{1}$=6,
∴在第1次抽到黑球的条件下,第2次抽到黑球的概率P(B|A)=$\frac{n}{m}$=$\frac{AB}{A}$=$\frac{6}{12}$=$\frac{1}{2}$.
(2)设事件C表示“2球中至少有一个黑球”,事件D表示“2球都是黑球”.
则n(C)=${C}_{5}^{2}-{C}_{2}^{2}$=9,n(CD)=${C}_{3}^{2}$=3,
∴在已知其中一个球为黑球的条件下,另一个球也是黑球的概率P(D|C)=$\frac{n(CD)}{n(C)}$=$\frac{3}{9}$=$\frac{1}{3}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意条件概率的合理运用.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题

| A. | -2 | B. | 2 | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{4}{3})$ | B. | $(\frac{2}{3},1]$ | C. | $[\frac{2}{3},1]$ | D. | $[1,\frac{4}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
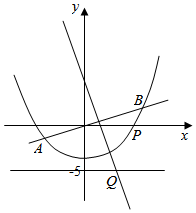 如图,直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4交于A,B两点,线段AB的垂直平分线与直线y=-5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为30.
如图,直线y=$\frac{1}{2}$x与抛物线y=$\frac{1}{8}$x2-4交于A,B两点,线段AB的垂直平分线与直线y=-5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为30.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com