
分析 分别构造函数f(x)=ln(x+1)-x,g(x)=ln(x+1)+$\frac{1}{x+1}$-1,根据函数的单调性求出函数的最值,从而证出结论.
解答 证明:(1)构造函数f(x)=ln(x+1)-x,
∵f′(x)=$\frac{-x}{x+1}$,(x>-1),当x=0,f′(0)=0,得下表
| x | -1<x<0 | 0 | x>0 |
| f′(x) | + | 0 | - |
| f(x) | 单调递增 | 极大值f(0)=0 | 单调递减 |
点评 本题主要考查利用导数研究函数的单调性,根据函数的单调性求函数的最值,体现了转化的数学思想,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
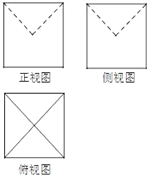 某几何体的三视图如图所示,图中的四边形都是边长为6的正方形,两条虚线互相垂直,则该几何体的体积是 ( )
某几何体的三视图如图所示,图中的四边形都是边长为6的正方形,两条虚线互相垂直,则该几何体的体积是 ( )| A. | 96 | B. | 108 | C. | 180 | D. | 198 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{5}$,1) | B. | [-$\sqrt{5}$,1) | C. | [-2,1) | D. | (-$\sqrt{5}$,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 250 | C. | 55 | D. | 133 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com