
分析 令t=2x+y,则y=-2x+t,t>0,代入4x2-2xy+y2=1得12x2-6tx+t2-1=0,由△=36t2-48(t2-1)≥0,结合4x2+4xy+y2=1+6xy>1,即(2x+y)2>1,解关于2x+y的不等式可得2x+y的取值范围;
令t=2x-y,则y=2x-t,代入4x2-2xy+y2=1得:4x2-2tx+t2-1=0,由△=4t2-16(t2-1)≥0,结合4x2-4xy+y2=1-2xy<1,即(2x-y)2<1,解关于2x-y的不等式可得2x-y的取值范围;
解答 解:令t=2x+y,则y=-2x+t,t>0,
代入4x2-2xy+y2=1得:4x2-2x(-2x+t)+(-2x+t)2=1,
即12x2-6tx+t2-1=0,
由△=36t2-48(t2-1)≥0得:t∈[-2,2],
又由4x2+4xy+y2=1+6xy>1,即(2x+y)2>1,
解得:2x+y∈(1,+∞),
故2x+y∈(1,2],
同理令t=2x-y,则y=2x-t,
代入4x2-2xy+y2=1得:4x2-2x(2x-t)+(2x-t)2=1,
即4x2-2tx+t2-1=0,
由△=4t2-16(t2-1)≥0得:t∈[-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$],
又由4x2-4xy+y2=1-2xy<1,即(2x-y)2<1,
解得:2x-y∈(-1,1),
故2x-y∈(-1,1),
故答案为:(1,2],(-1,1)
点评 本题考查了基本不等式的应用问题,也考查了不等式的解法与应用问题,是综合性题目


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | 2:1 | B. | 5:2 | C. | 1:4 | D. | 3:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
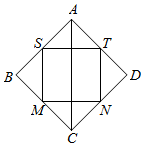 如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )| A. | 8:1 | B. | 2:1 | C. | 4:3 | D. | 8:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{2}{3},\;\frac{4}{3}}]$ | B. | $[{\frac{2}{3},\;+∞})$ | C. | $[{\frac{4}{3},\;+∞})$ | D. | $[{\frac{4}{3},\;+∞}]∪\left\{{\frac{2}{3}}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
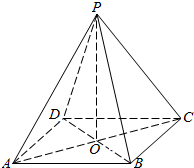 如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:
如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{5}$ | B. | $\frac{9}{5}$ | C. | $\frac{8}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com