
【题目】已知椭圆![]() .
.
(1)若椭圆![]() 的右焦点坐标为
的右焦点坐标为![]() ,求
,求![]() 的值;
的值;
(2)由椭圆![]() 上不同三点构成三角形称为椭圆的内接三角形.若以
上不同三点构成三角形称为椭圆的内接三角形.若以![]() 为直角顶点的椭圆
为直角顶点的椭圆![]() 的内接等腰直角三角形恰有三个,求
的内接等腰直角三角形恰有三个,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)本问考查椭圆标准方程,先将椭圆方程化为标准形式, 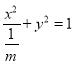 ,根据右焦点为
,根据右焦点为![]() ,则
,则![]() ,可以求出
,可以求出![]() 的值;(2)本问考查直线与椭圆位置关系,由题分析
的值;(2)本问考查直线与椭圆位置关系,由题分析![]() ,则
,则![]() ,因此BA所在直线斜率存在且不为0,可设
,因此BA所在直线斜率存在且不为0,可设![]() 的方程为
的方程为![]() ,将直线方程与椭圆方程联立,根据弦长公式求出
,将直线方程与椭圆方程联立,根据弦长公式求出![]() ,同理BC所在直线方程为
,同理BC所在直线方程为![]() ,同理求出
,同理求出![]() ,根据等腰直角三角形有
,根据等腰直角三角形有![]() ,整理得到关于
,整理得到关于![]() 的关系式,转化为以
的关系式,转化为以![]() 为变量的方程有两个不相等的正实根问题,求
为变量的方程有两个不相等的正实根问题,求![]() 的取值范围.
的取值范围.
试题解析:(1)椭圆![]() 的方程可以写成
的方程可以写成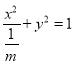 ,因为焦点
,因为焦点![]() 在
在![]() 轴上,所以
轴上,所以![]() ,求得
,求得![]() .
.
(2)设椭圆![]() 内接等腰直角三角形的两直角边分别为
内接等腰直角三角形的两直角边分别为![]() 设
设![]() ,显然
,显然![]() 与
与![]() 不与坐标轴平行,且
不与坐标轴平行,且![]() ,所以可设直线
,所以可设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,由
,由![]() ,消去
,消去![]() 得到
得到![]() ,所以
,所以![]() ,求得
,求得![]() .同理可求
.同理可求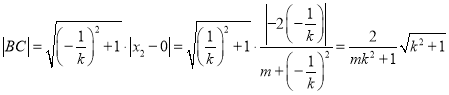 ,因为
,因为![]() 为以
为以![]() 为直角顶点的等腰直角三角形,所以
为直角顶点的等腰直角三角形,所以![]() .所以
.所以![]() ,整理得
,整理得
![]() ,所以
,所以![]() ,由此
,由此
![]() ,所以
,所以![]() 或
或![]() ,设
,设![]() ,因为以
,因为以![]() 为直角顶点的椭圆内接等腰直角三角形恰有三个,所以关于
为直角顶点的椭圆内接等腰直角三角形恰有三个,所以关于![]() 的方程
的方程![]() 有两个不同的正实根
有两个不同的正实根![]() ,且都不为
,且都不为![]() .所以
.所以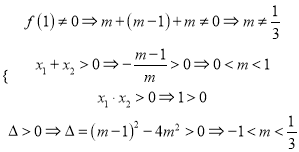 ,解得实数
,解得实数![]() 的取值范围是
的取值范围是![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知袋中装有大小相同的2个白球、2个红球和1个黄球.一项游戏规定:每个白球、红球和黄球的分值分别是0分、1分和2分,每一局从袋中一次性取出三个球,将3个球对应的分值相加后称为该局的得分,计算完得分后将球放回袋中.当出现第![]() 局得
局得![]() 分(
分(![]() )的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
)的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
(1)求在一局游戏中得3分的概率;
(2)求游戏结束时局数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1.设命题p:函数y=loga(x+1)在(0,+∞)内单调递减;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.若p或q为真,p且q为假,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2015高考湖北(理)20】某厂用鲜牛奶在某台设备上生产![]() 两种奶制品.生产1吨
两种奶制品.生产1吨![]() 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨
产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨![]() 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天
产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天![]() 产品的产量不超过
产品的产量不超过![]() 产品产量的2倍,设备每天生产
产品产量的2倍,设备每天生产![]() 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利![]() (单位:元)是一个随机变量.
(单位:元)是一个随机变量.
(Ⅰ)求![]() 的分布列和均值;
的分布列和均值;
(Ⅱ) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() 的图象经过点A(1,1),B(2,﹣1).
的图象经过点A(1,1),B(2,﹣1).
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并用定义证明;
(3)求f(x)在区间[ ![]() ,1]上的值域.
,1]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,有下列说法:
①若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上没有零点;
②若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上可能有零点;
③若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上没有零点;
④若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上至少有一个零点;
其中正确说法的序号是(把所有正确说法的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() :
: ![]() 与椭圆
与椭圆![]() :
: ![]() 在第一象限的交点为
在第一象限的交点为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 为椭圆的右顶点,
为椭圆的右顶点, ![]() 的面积为
的面积为![]() .
.
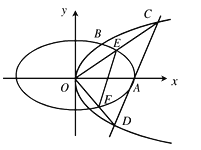
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作直线
点作直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() 两点,记
两点,记![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() ,问是否存在直线
,问是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x+2cos2x+m(0≤x≤
sin2x+2cos2x+m(0≤x≤ ![]() ).
).
(1)若函数f(x)的最大值为6,求常数m的值;
(2)若函数f(x)有两个零点x1和x2 , 求m的取值范围,并求x1和x2的值;
(3)在(1)的条件下,若g(x)=(t﹣1)f(x)﹣ ![]() (t≥2),讨论函数g(x)的零点个数.
(t≥2),讨论函数g(x)的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com