
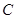 :
: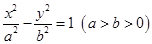 和圆
和圆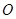 :
: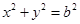 (其中原点
(其中原点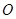 为圆心),过双曲线上一点
为圆心),过双曲线上一点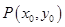 引圆
引圆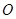 的两条切线,切点分别为
的两条切线,切点分别为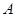 、
、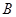 .
.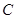 上存在点
上存在点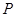 ,使得
,使得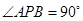 ,求双曲线离心率
,求双曲线离心率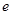 的取值范围;
的取值范围;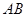 的方程;
的方程;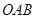 面积的最大值.
面积的最大值.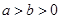 ,所以
,所以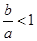 ,所以
,所以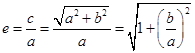
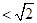 . 1分
. 1分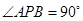 及圆的性质,可知四边形
及圆的性质,可知四边形 是正方形,所以
是正方形,所以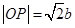 .
.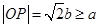 ,所以
,所以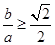 ,所以
,所以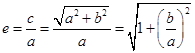
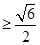 .3分
.3分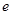 的取值范围为
的取值范围为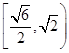 . 4分
. 4分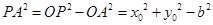 ,
,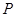 为圆心,
为圆心,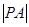 为半径的圆
为半径的圆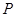 的方程为
的方程为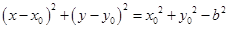 . 5分
. 5分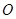 与圆
与圆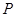 两圆的公共弦所在的直线即为直线
两圆的公共弦所在的直线即为直线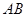 , 6分
, 6分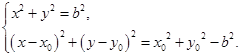 7分
7分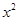 ,
,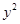 ,即得直线
,即得直线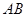 的方程为
的方程为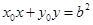 . 8分
. 8分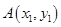
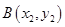 ,已知点
,已知点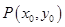 ,
,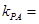
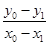 ,
,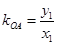
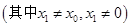 .
.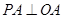 ,所以
,所以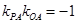 ,即
,即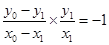 . 5分
. 5分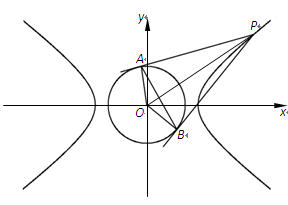
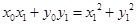 .
.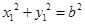 ,所以
,所以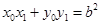 . 6分
. 6分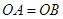 ,
,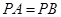 ,根据平面几何知识可知,
,根据平面几何知识可知,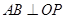 .
.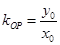 ,所以
,所以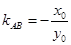 . 7分
. 7分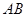 方程为
方程为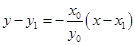 .
.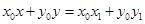 .
.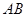 的方程为
的方程为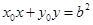 . 8分
. 8分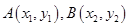 ,已知点
,已知点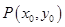 ,
,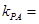
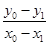 ,
,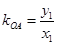
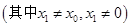 .
.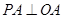 ,所以
,所以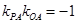 ,即
,即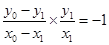 . 5分
. 5分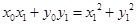 .
.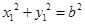 ,所以
,所以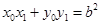 . 6分
. 6分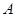 在直线
在直线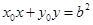 上. 7分
上. 7分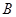 也在直线
也在直线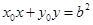 上.
上.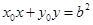 就是直线
就是直线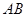 的方程. 8分
的方程. 8分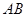 的方程为
的方程为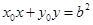 ,
,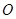 到直线
到直线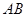 的距离为
的距离为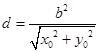 .
.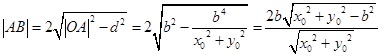 ,
,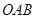 的面积
的面积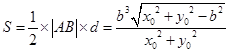 . 10分
. 10分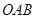 的面积
的面积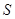 的三种方法:
的三种方法: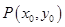 在双曲线
在双曲线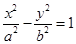 上,
上,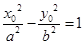 ,即
,即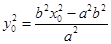
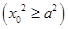 .
.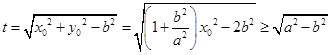 ,
,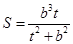 . 11分
. 11分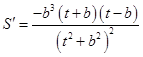 ,
,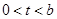 时,
时,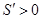 ,当
,当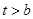 时,
时,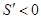 .
.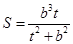 在
在 上单调递增,在
上单调递增,在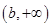 上单调递减. 12分
上单调递减. 12分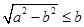 ,即
,即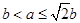 时,
时,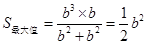 , 13分
, 13分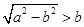 ,即
,即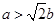 时,
时,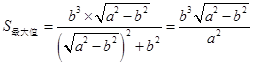 .
.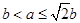 时,
时,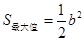 ;当
;当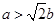 时,
时,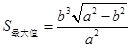 . 14分
. 14分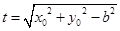 ,则
,则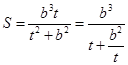 . 11分
. 11分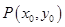 在双曲线
在双曲线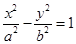 上,即
上,即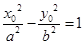 ,即
,即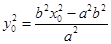
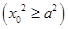 .
.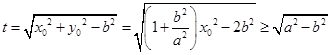 .
.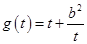 ,则
,则 .
.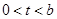 时,
时,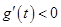 ,当
,当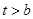 时,
时,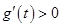 .
.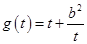 在
在 上单调递减,在
上单调递减,在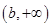 上单调递增. 12分
上单调递增. 12分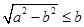 ,即
,即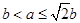 时,
时,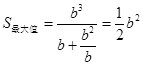 , 13分
, 13分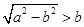 ,即
,即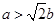 时,
时,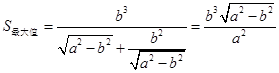 .
.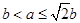 时,
时,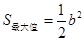 ;当
;当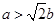 时,
时,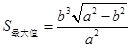 . 14分
. 14分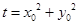 ,则
,则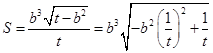 . 11分
. 11分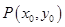 在双曲线
在双曲线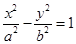 上,即
上,即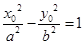 ,即
,即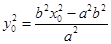
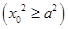 .
.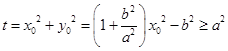 .
.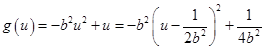 ,
,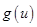 在
在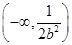 上单调递增,在
上单调递增,在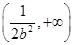 上单调递减. 12分
上单调递减. 12分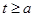 ,所以
,所以 ,
,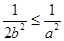 ,即
,即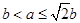 时,
时,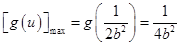 ,此时
,此时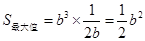 .
.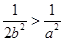 ,即
,即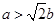 时,
时,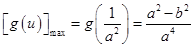 ,此时
,此时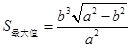 .
.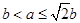 时,
时,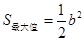 ;当
;当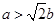 时,
时,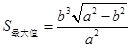 . 14分
. 14分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com