Question

11．已知抛物线C：y²=8x，点P为抛物线上任意一点，过点P向圆D：x²+y²-4x+3=0作切线，切点分别为A，B，则四边形PADB面积的最小值为（　　）

• A． $\sqrt{2}$
• B． $\sqrt{3}$
• C． 2
• D． 3

Answer 1

分析 设P（x，y），D为抛物线的焦点，故而PD=x+2，利用勾股定理求出PA，得出四边形面积关于x的函数，利用二次函数的性质及x的范围得出面积的最小值．

解答 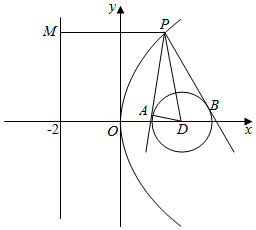解：圆D的圆心为D（2，0），半径为r=DA=1，
与抛物线的焦点重合．
抛物线的准线方程为x=-2．
设P（x，y），
则由抛物线的定义可知PD=PM=x+2，
∵PA为圆D的切线，
∴PA⊥AD，
∴PA=$\sqrt{P{D}^{2}-A{D}^{2}}$=$\sqrt{{x}^{2}+2x+3}$．
∴S_{四边形PADB}=2S_△PAD=2×$\frac{1}{2}$AD×PA
=$\sqrt{{x}^{2}+2x+3}$．
∵x≥0，∴当x=0时，S_{四边形PADB}取得最小值$\sqrt{3}$．
故选B．

点评 本题考查了抛物线的性质，圆的切线的性质，属于中档题．