Question

11．求函数y=$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}+2x+10}$的值域．

Answer 1

分析 将原函数变成y=$\sqrt{（x-0）^{2}+（0-2）^{2}}+\sqrt{[x-（-1）]^{2}+（0-3）^{2}}$，这样便可将y看成x轴上的点到点（0，2）和点（-1，3）距离的和，可设A（-1，3），B（0，2），作A点关于x轴的对称点，连接BC，从而|BC|便是y的最小值，容易知道y可趋于正无穷，这样便可写出函数的值域．

解答 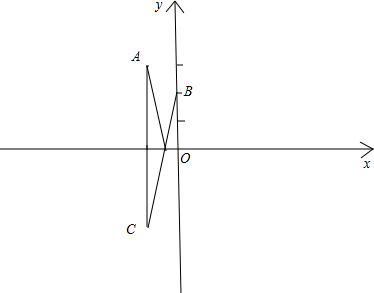解：显然该函数的定义域为R；
原函数变成：$y=\sqrt{（x-0）^{2}+（0-2）^{2}}$+$\sqrt{[x-（-1）]^{2}+（0-3）^{2}}$；
∴y表示点（x，0）到点（0，2）的距离和它到（-1，3）距离的和；
如图，设A（-1，3），B（0，2），作A关于x轴的对称点C（-1，-3），连接BC，则：
|BC|便是点（x，0）到A点，B点和的最小值；
|BC|=$\sqrt{（0+1）^{2}+（2+3）^{2}}=\sqrt{26}$；
∴$y∈[\sqrt{26}，+∞）$；
即原函数的值域为[$\sqrt{26}，+∞$）．

点评 考查平面上两点间的距离公式，几何的方法求函数值域，掌握求x轴上的点到平面上两点距离和的最小值的方法．