
分析 根据正弦定理以及倍角公式先求出cosA,然后结合余弦定理求出b,利用向量的定义进行求解.
解答 解:∵sin2A=sinC,
∴2sinAcosA=sinC,
即cosA=$\frac{sinC}{2sinA}=\frac{c}{2a}$=$\frac{1}{6}$,
又a2=b2+c2-2bccosA,
即9=b2+1-2b×1×$\frac{1}{6}$,
即3b2-b-24=0,
解得b=3或b=-$\frac{8}{3}$(舍),
则$\overrightarrow{AB}•\overrightarrow{AC}$=bccosA=3×$1×\frac{1}{6}=\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查平面向量数量积的计算,利用正弦定理和余弦定理求出cosA和b是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 0.6826 | B. | 0.3413 | C. | 0.0026 | D. | 0.4772 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x/百万元 | 2 | 4 | 5 | 6 | 8 |
| y/百万元 | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
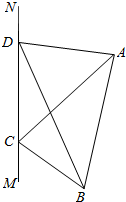 如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.
如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com