
分析 (1)直线方程可整理为(x-2y+2)+(4x+3y-14)k=0,可得直线过定点;求出圆心C到点P(2,2)的距离,与半径比较,可得可得直线l1与圆的位置关系;
(2)$AB+EF=2\sqrt{16-{d_2}^2}+2\sqrt{16-{d_1}^2}$,利用基本不等式,即可求AB+EF的最大值.
解答 解:(1)直线与圆相交…(2分)
证明:直线方程可整理为(x-2y+2)+(4x+3y-14)k=0
所以$\left\{{\begin{array}{l}{x-2y+2=0}\\{4x+3y-14=0}\end{array}}\right.$解得$\left\{{\begin{array}{l}{x=2}\\{y=2}\end{array}}\right.$
所以直线过定点P(2,2)…(5分)
圆C方程可整理为(x-3)2+(y-4)2=16
因为圆心C到点P(2,2)的距离d为$d=\sqrt{1+4}=\sqrt{5}$
由$d=\sqrt{5}<4$,所以直线与圆C相交…(6分)
(2)设点C到直线AB,EF的距离分别为d1,d2(d1,d2≥0)
则$d_1^2+d_2^2=5$…(8分)
又$AB=2\sqrt{16-{d_1}^2},EF=2\sqrt{16-{d_2}^2}$
所以$AB+EF=2\sqrt{16-{d_2}^2}+2\sqrt{16-{d_1}^2}$…(10分)
则$\begin{array}{l}{(AB+EF)^2}={(2\sqrt{16-{d_2}^2}+2\sqrt{16-{d_1}^2})^2}\end{array}$=$4(16-{d_1}^2+16-{d_2}^2+2\sqrt{16-{d_1}^2}•\sqrt{16-{d_2}^2})$
=$4(27+2\sqrt{256-16(d_1^2+d_2^2)+d_1^2•d_2^2}$
=$4(27+2\sqrt{176+d_1^2•d_2^2}$…(12分)
又因为$2d_1^{\;}d_2^{\;}≤d_1^2+d_2^2=5$
所以$d_1^2d_2^2≤\frac{25}{4}$(当且仅当$d_1^{\;}={d_2}=\frac{{\sqrt{10}}}{2}$时取到等号)…(14分)
所以 $\sqrt{176+d_1^2•d_2^2}≤\sqrt{176+\frac{25}{4}}=\sqrt{\frac{729}{4}}=\frac{27}{2}$
所以${(AB+EF)^2}≤4(27+2×\frac{27}{2})=216$
所以$AB+EF≤6\sqrt{6}$
所以AB+EF的最大值为$6\sqrt{6}$…(16分)
点评 本题考查直线与圆的位置关系,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2} | C. | {0,1,2,3} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
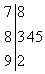 如图是某校高二年级举办的歌咏比赛上,五位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{2}{3}$.
如图是某校高二年级举办的歌咏比赛上,五位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-3)<f(-5) | B. | f(-3)>f(-5) | C. | f(-3)<f(5) | D. | f(-3)=f(-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com