
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
分析 令x+$\frac{1}{x}$-2=t,则f(t)=a,结合f(x)的函数图象可知关于t的方程f(t)=a的解的个数和解的范围,利用t的范围得出关于x的方程x+$\frac{1}{x}$-2=t的解的个数即可得出答案.
解答 解:令x+$\frac{1}{x}$-2=t,则f(t)=a,
做出y=f(x)的函数图象如图所示:
由图象可知:当1<a<2时,关于t的方程f(t)=a有3解.
不妨设3个解分别为t1,t2,t3,且t1<t2<t3,
则-24<t1<-4,1<t2<2,2<t3<3,
当x+$\frac{1}{x}$-2=t1,即x2-(2+t1)x+1=0,
∵-24<t1<-4,
∴△=(2+t1)2-4>0,
∴方程x+$\frac{1}{x}$-2=t1有2解,
同理:方程x+$\frac{1}{x}$-2=t2有2解,x+$\frac{1}{x}$-2=t3有2解,
∴当1<a<2时,关于x的方程$f({x+\frac{1}{x}-2})=a$有6解.
故选B.
点评 本题考查了函数的零点的个数判断与函数图象的关系,属于中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [1,2) | C. | (0,1] | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | $±\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $±\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{100}$”表示成“$\sum_{k=1}^{100}{\frac{1}{k}}$” | |
| B. | 平面上所有二次曲线的一般形式均可表示成:Ax2+Bxy+Cy2+Dx+Ey+F=0 | |
| C. | 正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$ | |
| D. | 123456789×9+10=1111111111 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
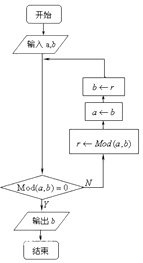 辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.
辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com