
| A. | (1,2) | B. | (2,2$\sqrt{2}$) | C. | (3,2$\sqrt{3}$) | D. | (4,4) |
分析 由抛物线方程求出焦点坐标,设出E的坐标(-1,m),利用EF和QP垂直求得m的值,则QP的方程可求,联立QP的方程与抛物线方程即可求出P的坐标.
解答 解:如图, 由抛物线方程为y2=4x,得F(1,0),设E(-1,m)(m>0),
由抛物线方程为y2=4x,得F(1,0),设E(-1,m)(m>0),
则EF中点为G(0,$\frac{m}{2}$),${k}_{EF}=-\frac{m}{2}$,又Q(-1,$\frac{3}{2}$),
∴${k}_{QG}=\frac{\frac{3}{2}-\frac{m}{2}}{-1-0}=\frac{m-3}{2}$,则$-\frac{m}{2}•\frac{m-3}{2}=-1$,解得:m=4.
∴${k}_{OG}=\frac{4-3}{2}=\frac{1}{2}$,则QG所在直线方程为y-$\frac{3}{2}$=$\frac{1}{2}(x+1)$,即x-2y+4=0.
联立$\left\{\begin{array}{l}{x-2y+4=0}\\{{y}^{2}=4x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,即P(4,4),
故选:D.
点评 本题考查了抛物线的简单性质,考查了抛物线的应用,平面解析式的基础知识.考查了考生的基础知识的综合运用和知识迁移的能力,是中档题.


科目:高中数学 来源: 题型:解答题
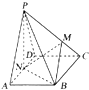 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.
如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设平行于y轴的直线分别与函数y1=log2x及y2=log2x+2的图象交于B,C两点,点A(m,n)位于函数y2的图象上,若△ABC为正三角形,则m•2n=( )
设平行于y轴的直线分别与函数y1=log2x及y2=log2x+2的图象交于B,C两点,点A(m,n)位于函数y2的图象上,若△ABC为正三角形,则m•2n=( )| A. | 8$\sqrt{3}$ | B. | 12 | C. | 12$\sqrt{3}$ | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com