
分析 由题意可设直线MN的方程为y=kx+2,M (x1,x2),N(x2,y2),MN 的中点E(x0,y0),联立方程可得x2+8kx+16=0,由△>0可求k的范围,由方程的根与系数关系及中点坐标公式可求MN的中点E,由即BE⊥MN即M在MN的垂直平分线,则MN的垂直平分线与y轴的交点即是B,令x=0可求B的纵坐标,结合K的范围可求|$\overrightarrow{OB}$|的范围
解答 解:由题意可得A(0,2),直线MN的斜率k存在且k≠0
设直线MN的方程为y=kx+2,M (x1,x2),N(x2,y2),MN 的中点E(x0,y0),
联立方程$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}=-8y}\end{array}\right.$可得x2+8kx+16=0
则可得,△=64k2-64>0,即k2>1,x1+x2=-8k,y1+y2=k(x1+x2)+4=4-8k2
∴x0=$\frac{1}{2}$(x1+x2)=-4k,y0=$\frac{1}{2}$(y1+y2)=2-4k2即E(-4k,2-4k2)
又2$\overrightarrow{BM}$+$\overrightarrow{MN}$=2$\overrightarrow{BM}$+2$\overrightarrow{ME}$=2$\overrightarrow{BE}$,
∵(2$\overrightarrow{BM}$+$\overrightarrow{MN}$)⊥$\overrightarrow{MN}$,即BE⊥MN即M在MN的垂直平分线
则MN的垂直平分线y+4k2-2=-$\frac{1}{k}$(x+4k)与y轴的交点即是B,
令x=0可得,y=-2-4k2
则|$\overrightarrow{OB}$|=2+4k2>6
故答案为(6,+∞).
点评 本题主要考查了向量的数量积的性质的应用,直线与抛物线的相交关系的应用,方程的根与系数关系的应用,属于向量知识的综合应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
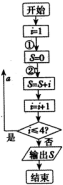 执行如图所示的程序框图.设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出S的值为n,则m+n=( )
执行如图所示的程序框图.设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出S的值为n,则m+n=( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com