
已知函数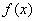 是定义在
是定义在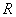 上的奇函数,当
上的奇函数,当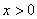 时,
时,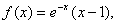 给出以下命题:
给出以下命题:
①当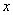
 时,
时,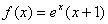 ; ②函数
; ②函数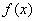 有五个零点;
有五个零点;
③若关于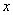 的方程
的方程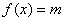 有解,则实数
有解,则实数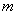 的取值范围是
的取值范围是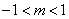 ;
;
④对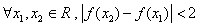 恒成立.
恒成立.
其中,正确命题的序号是 .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
如图,先将边长为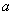 的正方形铁皮的四个角各截去一个边长为
的正方形铁皮的四个角各截去一个边长为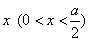 的小正方形,然后沿虚线折成一个无盖的长方体盒子.设长方体盒子的体积是
的小正方形,然后沿虚线折成一个无盖的长方体盒子.设长方体盒子的体积是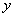 ,则
,则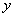 关于
关于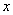 的函数关系式为
的函数关系式为
A. B.
B.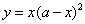
C.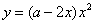 D.
D.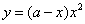

查看答案和解析>>
科目:高中数学 来源: 题型:
.小强和小华两位同学约定下午在武荣公园篮球场见面,约定谁先到后必须等10分钟,这时若
另一人还没有来就可以离开.如果小强是1:40分到达的,假设小华在1点到3点内到达,且
小华在 1点到3点之间何时到达是等可能的,则他们会面的概率是
A.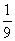 B.
B.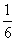 C.
C. 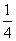 D.
D.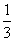
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形
且∠A1AC=∠DAB=60o,平面AA1C1C⊥平面ABCD.(Ⅰ)证明:BD⊥AA1;
(Ⅱ)证明:平面AB1C∥平面DA1C1;
(Ⅲ)在棱CC1上是否存在点P,使得平面PDA1和平面DA1C1所成锐二面角的余弦值为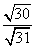 ?若存在,求出点P的位置;若不存在,说明理由.
?若存在,求出点P的位置;若不存在,说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com