
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形
且∠A1AC=∠DAB=60o,平面AA1C1C⊥平面ABCD.(Ⅰ)证明:BD⊥AA1;
(Ⅱ)证明:平面AB1C∥平面DA1C1;
(Ⅲ)在棱CC1上是否存在点P,使得平面PDA1和平面DA1C1所成锐二面角的余弦值为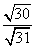 ?若存在,求出点P的位置;若不存在,说明理由.
?若存在,求出点P的位置;若不存在,说明理由.
 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
若函数h(x)=2x-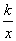 +
+ 在(1,+∞)上是增函数,则实数k的取值范围是( ).
在(1,+∞)上是增函数,则实数k的取值范围是( ).
A.[1,+∞) B. (-2,+∞) C.[-2,2] D. [-2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数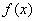 是定义在
是定义在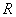 上的奇函数,当
上的奇函数,当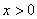 时,
时,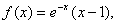 给出以下命题:
给出以下命题:
①当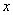
 时,
时,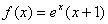 ; ②函数
; ②函数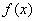 有五个零点;
有五个零点;
③若关于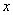 的方程
的方程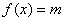 有解,则实数
有解,则实数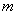 的取值范围是
的取值范围是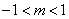 ;
;
④对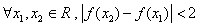 恒成立.
恒成立.
其中,正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明命题 “自然数a、b 、c中恰有一个偶数”时,需假设原命题不成立,下列假设正确的是( )
A.a、b、c都是奇数 B.a、b 、c都是偶数
C.a、b、c中或都是奇数或至少有两个偶数 D.a、b 、c中至少有两个偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
平面几何中,有边长为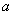 的正三角形内任一点到三边距离之和为定值
的正三角形内任一点到三边距离之和为定值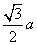 ,类比上述命题,棱长为
,类比上述命题,棱长为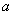 的正四面体内任一点到四个面的距离之和为( )
的正四面体内任一点到四个面的距离之和为( )
A.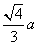 B.
B. C.
C. D.
D.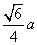
查看答案和解析>>
科目:高中数学 来源: 题型:
有以下命题:
①如果向量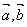 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么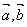 的关系是不共线;
的关系是不共线;
②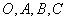 为空间四点,且向量
为空间四点,且向量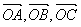 不构成空间的一个基底,则点
不构成空间的一个基底,则点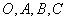 一定共面;
一定共面;
③已知向量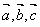 是空间的一个基底,则向量
是空间的一个基底,则向量 也是空间的一个基底其中正确的命题是 ( )
也是空间的一个基底其中正确的命题是 ( )
(A)①② (B)①③ (C)②③ (D)①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com