
���� ��1��ѡ��һ�����û��¼��ĸ��ʹ�ʽ������λ�˿;����ܵ��ⵥ�ĸ���ֵ��
��2��ѡ��һ��������������X�ķֲ��к���ѧ����ֵ��
ѡ������������������Z����ѧ����ֵ���Ƚϵó����ۣ�
��� �⣺��1��ѡ��һ�������ܵ��ⵥ�Żݣ�����Ҫ����3������
��˿����ܵ��ⵥ�Ż�Ϊ�¼�A����
$P��A��=\frac{C_3^3}{{C_{10}^3}}=\frac{1}{120}$��
������λ�˿;����ܵ��ⵥ�ĸ���Ϊ
$P=P��A��•P��A��=\frac{1}{14400}$��
��2����ѡ��һ���踶����ΪXԪ����
X���ܵ�ȡֵΪ0��600��700��1000��
����$P��{X=0}��=\frac{C_3^3}{{C_{10}^3}}=\frac{1}{120}��P��{X=600}��=\frac{C_3^2C_7^1}{{C_{10}^3}}=\frac{7}{40}$��
$P��{X=700}��=\frac{C_3^1C_7^2}{{C_{10}^3}}=\frac{21}{40}��P��{X=1000}��=\frac{C_7^3}{{C_{10}^3}}=\frac{7}{24}$��
��X�ķֲ���Ϊ��
| X | ��0 | ��600 | 700 | 1000 |
| ��P | $\frac{1}{120}$ | $\frac{7}{40}$ | $\frac{21}{40}$ | $\frac{7}{24}$ |
���� ���⿼������ɢ����������ķֲ�������ѧ�����ļ������⣬���е��⣮


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 2 | C�� | 1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{5}$ | B�� | -$\frac{7}{5}$ | C�� | $-\frac{1}{5}$ | D�� | $\frac{7}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
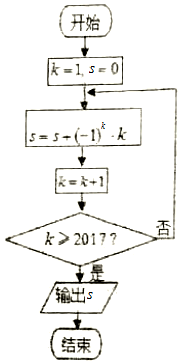
| A�� | 2017 | B�� | 2016 | C�� | 1009 | D�� | 1008 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 6+4$\sqrt{2}$ | B�� | 4+4$\sqrt{2}$ | C�� | 2 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
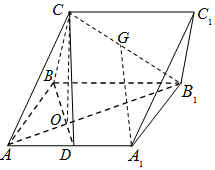 ��������ABC-A1B1C1�У�����ABB1A1Ϊ���Σ�AB=2��AA1=2$\sqrt{2}$��D��AA1���е㣬BD��AB1���ڵ�O����OC��ƽ��ABB1A1��
��������ABC-A1B1C1�У�����ABB1A1Ϊ���Σ�AB=2��AA1=2$\sqrt{2}$��D��AA1���е㣬BD��AB1���ڵ�O����OC��ƽ��ABB1A1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com