
|
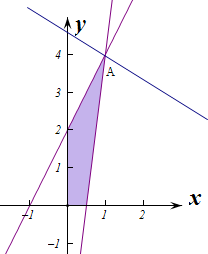 解:由z=ax+by(a>0,b>0)得y=-
解:由z=ax+by(a>0,b>0)得y=-| a |
| b |
| z |
| b |
| a |
| b |
| a |
| b |
| z |
| b |
| a |
| b |
| z |
| b |
| a |
| b |
| z |
| b |
|
|
| 4ab |
| ab |
| ab |


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
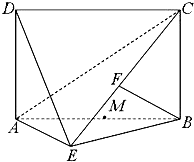 四边形ABCD为矩形,∠AEB=
四边形ABCD为矩形,∠AEB=| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 1 |
| {an} |
查看答案和解析>>
科目:高中数学 来源: 题型:
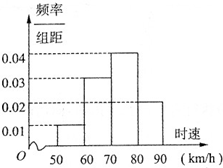 某地区对某路段公路上行驶的汽车速度实施监控,从中抽取50辆汽车进行测速分析,得到如图所示的时速的频率分布直方图,根据该图,时速在70km/h以下的汽车有
某地区对某路段公路上行驶的汽车速度实施监控,从中抽取50辆汽车进行测速分析,得到如图所示的时速的频率分布直方图,根据该图,时速在70km/h以下的汽车有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com