
分析 (1)根据生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和,可建立函数关系式;
(2)利用换元法,再借助于基本不等式,即可求得最值.
解答 解:(1)由题意可得,产品的生产成本为(32Q+3)万元,
每万件销售价为$\frac{32Q+3}{Q}×150%+\frac{x}{Q}×50%$,(2分)
∴年销售收入为$({\frac{32Q+3}{Q}×150%+\frac{x}{Q}×50%})•Q$=$\frac{3}{2}(32Q+3)+\frac{1}{2}x$,(4分)
∴年利润$W=\frac{3}{2}(32Q+3)+\frac{1}{2}x-(32Q+3)-x$=$\frac{1}{2}(32Q+3-x)=\frac{{-{x^2}+98x+35}}{2(x+1)}(x≥0)$.(6分)
(2)令x+1=t(t≥1),则$W=\frac{{-{{(t-1)}^2}+98(t-1)+35}}{2t}=50-({\frac{t}{2}+\frac{32}{t}})$.(8分)
∵t≥1,∴$\frac{t}{2}+\frac{32}{t}≥2\sqrt{\frac{t}{2}•\frac{32}{t}}=8$,即W≤42,(10分)
当且仅当$\frac{t}{2}=\frac{32}{t}$,即t=8时,W有最大值42,此时x=7.
即当年广告费为7万元时,企业利润最大,最大值为42万元.(12分)
点评 本题考查的知识点是函数模型的选择与应用,利用利润=收入-成本,得到年利润的表达式是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $12\sqrt{3}$ | C. | $\sqrt{3}或2\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,0) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x<sinx且x>tanx | B. | ?x∈R,x≥sinx或x≤tanx | ||
| C. | ?x∈R,x<sinx或x>tanx | D. | ?x∈R,x≥sinx且x≤tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
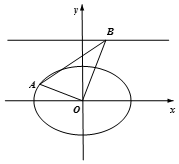 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),离心率为$\frac{{\sqrt{2}}}{2}$,左准线方程是x=-2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),离心率为$\frac{{\sqrt{2}}}{2}$,左准线方程是x=-2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com