
分析 (1)根据解析式中分母不为0,求出函数f(x)的定义域;
(2)根据奇偶性的定义判断f(x)是定义域上的奇函数.
解答 解:(1)函数$f(x)=\frac{1}{{{3^x}-1}}+\frac{1}{2}$,
∴3x-1≠0,解得x≠0;
∴f(x)的定义域为(-∞,0)∪(0,+∞);
(2)f(x)的定义域关于原点对称,
且f(-x)+f(x)=($\frac{1}{{3}^{-x}-1}$+$\frac{1}{2}$)+($\frac{1}{{3}^{x}-1}$+$\frac{1}{2}$)
=$\frac{{3}^{x}}{1{-3}^{x}}$+$\frac{1}{{3}^{x}-1}$+1
=-1+1
=0;
∴f(x)是定义域(-∞,0)∪(0,+∞)上的奇函数.
点评 本题考查了求函数的定义域和判断奇偶性问题,是基础题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一或第二象限 | B. | 第二或第三象限 | C. | 第一或第三象限 | D. | 第二或第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
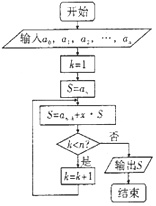 秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )
秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )| A. | 248 | B. | 258 | C. | 268 | D. | 278 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
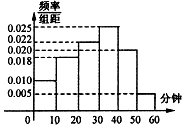 北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.| 非围棋迷 | 围棋迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(x2≥k0) | 0.05 | 0.010 |
| k0 | 3.74 | 6.63 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com