
【题目】对于定义域为![]() 的函数
的函数![]() ,如果存在区间
,如果存在区间![]() 满足
满足![]() 是
是![]() 上的单调函数,且
上的单调函数,且![]() 在区间
在区间![]() 上的值域也为
上的值域也为![]() ,则称函数
,则称函数![]() 为区间
为区间![]() 上的“保值函数”,
上的“保值函数”,![]() 为“保值区间”.根据此定义给出下列命题:①函数
为“保值区间”.根据此定义给出下列命题:①函数![]() 是
是![]() 上的“保值函数”;②若函数
上的“保值函数”;②若函数![]() 是
是![]() 上的“保值函数”,则
上的“保值函数”,则![]() ;③对于函数
;③对于函数![]() 存在区间
存在区间![]() ,且
,且![]() ,使函数
,使函数![]() 为
为![]() 上的“保值函数”.其中所有真命题的序号为( )
上的“保值函数”.其中所有真命题的序号为( )
A.②B.③C.①③D.②③
【答案】D
【解析】
①根据函数单调性定义和“保值函数”的概念判断即可,②结合函数![]() 的图象可得结论,③由导数确定函数在
的图象可得结论,③由导数确定函数在![]() 是单调递增的,而方程
是单调递增的,而方程![]() 有两个解
有两个解![]() (
(![]() ),构造新函数
),构造新函数![]() ,由零点存在定理确定
,由零点存在定理确定![]() 的零点
的零点![]() 即可.
即可.
由“保值函数”定义可知![]() 为区间
为区间![]() 上的“保值函数”则
上的“保值函数”则![]() 在
在![]() 上是单调函数且在区间
上是单调函数且在区间![]() 时其值域也为
时其值域也为![]() ,那么当函数
,那么当函数![]() 为增函数时满足条件
为增函数时满足条件![]() 在
在![]() 上有两个不同的实数解
上有两个不同的实数解![]() ,
,![]() 的函数
的函数![]() 就是“保值函数”,
就是“保值函数”,
命题①中![]() ,虽满足在
,虽满足在![]() 上单调但值域为
上单调但值域为![]() ,不是
,不是![]() ,故①为假命题;
,故①为假命题;
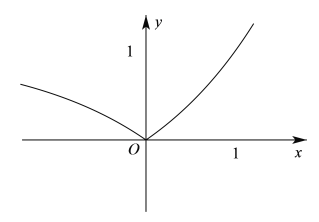
②中由![]() 的图象可知,函数在
的图象可知,函数在![]() 上单调且值域为
上单调且值域为![]() ,其为区间
,其为区间![]() 上的“保值函数”故②为真命题;
上的“保值函数”故②为真命题;
③中![]() ,则由
,则由![]() 在
在![]() 成立,所以
成立,所以![]() 为
为![]() 上的增函数,再由
上的增函数,再由![]() 解得有两个根
解得有两个根![]() ,
,![]() ,构造函数
,构造函数![]() ,
,![]() 是减函数,
是减函数,![]() ,
,![]() ,由零点存在性定理知存在
,由零点存在性定理知存在![]() ,使
,使![]() 成立,故③为真命题.综上所有真命题的序号为②③,
成立,故③为真命题.综上所有真命题的序号为②③,
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某网站举行“卫生防疫”的知识竞赛网上答题,共有120000人通过该网站参加了这次竞赛,为了解竞赛成绩情况,从中抽取了100人的成绩进行统计,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
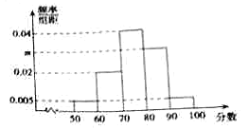
(1)求![]() 的值;
的值;
(2)成绩不低于90分的人就能获得积分奖励,求所有参赛者中获得奖励的人数;
(3)根据频率分布直方图,估计这次知识竞赛成绩的平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点为
的左右顶点为![]() ,
,![]() 为椭圆上异于
为椭圆上异于![]() 的动点,设直线
的动点,设直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)当椭圆![]() 内切于圆
内切于圆![]() 时,设动直线
时,设动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,问:
,问:![]() 的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科技创新能力是决定综合国力和国际竞争力的关键因素,也是推动经济实现高质量发展的重要支撑,而研发投入是科技创新的基本保障,下图是某公司从2010年到2019年这10年研发投入的数据分布图:

其中折线图是该公司研发投入占当年总营收的百分比,条形图是当年研发投入的数值(单位:十亿元).
(I)从2010年至2019年中随机选取一年,求该年研发投入占当年总营收的百分比超过10%的概率;
(II)从2010年至2019年中随机选取两个年份,设X表示其中研发投入超过500亿元的年份的个数,求X的分布列和数学期望;
(III)根据图中的信息,结合统计学知识,判断该公司在发展的过程中是否比较重视研发,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
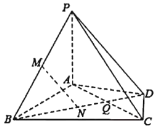
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,底面
的中点,底面![]() 是正三角形,延长
是正三角形,延长![]() 到点
到点![]() ,使得
,使得![]() .
.
(1)![]() 为线段
为线段![]() 上确定一点,当
上确定一点,当![]() 平面
平面![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 平面
平面![]() ,且
,且![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a∈R且a≠0).
(a∈R且a≠0).
(1)当a![]() 时,求曲线y=f(x)在点(1,f(1))处的切线方程;
时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性与单调区间;
(3)若y=f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)<9﹣lna.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆![]() (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(1)求椭圆的标准方程;
(2)若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2,求证:k1k2=e2﹣1(e为椭圆的离心率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.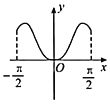
C.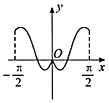 D.
D.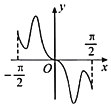
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,
中,![]() ,
,![]() 在边
在边![]() 上,
上,![]() .沿
.沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,使平面
折起,使平面![]() 和平面
和平面![]() 都与平面
都与平面![]() 垂直,如图(2).
垂直,如图(2).
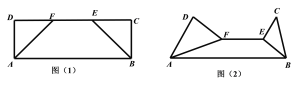
(1)试判断图(2)中直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求平面![]() 和平面
和平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com