练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
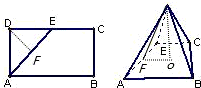
    如图，在矩形ABCD中，AB=6，BC=4，E是CD的中点，沿AE将△ADE折起，使二面角D-AE-B为60°，则四棱锥D-ABCE的体积是（　　）
    A、
    18
    5
    		3
    B、
    36
    5
    		3
    C、
    72
    5
    		3
    D、
    108
    5
    		3
    考点：棱柱、棱锥、棱台的体积
    专题：空间位置关系与距离
    分析：作出四棱锥的高，在侧面ABD上的斜高，从而构造了二面角D-AE-B，计算出高和底的面积，再用棱锥的体积公式化求解．
    解答： 解：如图，作DF⊥AE，DO⊥平面ABCD，连结OF，
    根据题意，∠DFO=60°，
    在△ADE中，DF=
    AD•DE
    AE
    =
    4×3
    		16+9
    =
    12
    5
    ，
    在△DFO中，DO=DF•sin60°=
    6
    		3
    5
    ，
    S四边形ABCE=
    1
    2
    (AB+CE)•BC    =18，
    ∴四棱锥D-ABCE的体积：
    V=
    1
    3
    S四边形ABCE•DO    =
    1
    3
    ×18×
    6
    		3
    5
    =
    36
    		3
    5
    ．
    故选：B．
    点评：本题考查四棱锥D-ABCE的体积的求法，考查平面图形和空间图形的转化，要注意前后的不变量和改变量．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    过棱长为a的正方体的三个顶点截下一个底面是等边三角形的棱锥，这个棱锥的表面积是（　　）
    A、（3+
    		3
    2
    ）a2
    B、
    3+
    		3
    2
    a2
    C、
    6+
    		3
    4
    a2
    D、
    3+
    		3
    4
    a2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=3x-2，x∈[-1，1]的值域是（　　）
    A、[1，
    5
    3
    ]
    B、[-1，1]
    C、[-
    5
    3
    ，1]
    D、[0，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    马先生于两年前购买了一部手机，现在这款手机的价格已降为1000元，设这种手机每年降价20%，那么两年前这部手机的价格为（　　）
    A、1535.5元
    B、1440元
    C、1620元
    D、1562.5元

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    ax，x≥2
    (3-a)x+2，x＜2
    ，满足对任意x1≠x2，都有
    f(x1)-f(x2)
    x1-x2
    ＜0，则实数a取值的范围是（　　）
    A、1＜a＜3
    B、2≤a＜3
    C、1＜a≤2
    D、2＜a＜3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    ，
    b
    ，
    c
    ，满足|
    a
    |=2，|
    a
    -
    b
    |=|
    b
    |，（
    a
    -
    c
    ）•（
    b
    -
    c
    ）=0，若对于每一确定的
    b
    ，|
    c
    |的最大值和最小值分别为m，n，则对任意
    b
    ，m-n的最小值是（　　）
    A、
    1
    4
    B、
    1
    2
    C、
    3
    4
    D、1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    空中有一气球，在它的正西方A点测得它的仰角为45°，同时在它南偏东60°的B点，测得它的仰角为30°，若A、B两点间的距离为266米，这两个观测点均离地1米，那么测量时气球到地面的距离是（　　）
    A、
    266
    		7
    7
    米
    B、（
    266
    		7
    7
    +1）米
    C、266米
    D、266
    		7
    米

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在集合{1，2，3，4，5，6}中任取一个偶数a和一个奇数b构成以原点为起点的向量
    a
    =（a，b），从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形，记所有作成的平行四边形的个数为t，在区间[1，
    t
    5
    ]和[2，4]分别各取一个数，记为m和n，则方程
    x 2
    m 2
    +
    y 2
    n 2
    =1表示焦点在x轴上的椭圆的概率是（　　）
    A、
    1
    3
    B、
    1
    2
    C、
    2
    3
    D、
    3
    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    每年春季在郑州举行的“中国郑开国际马拉松赛”活动，已成为最有影响力的全民健身活动之一，每年的参与人数不断增多，然后也有部分人对该活动的实际效果提出了疑问，对此，某新闻媒体进行了网上调查，在所有参与调查的人中，持“支持”、“保留意见”和“不支持”态度的人数如下表所示：
    支持保留意见不支持
    男800450200
    女100150300
    （Ⅰ）在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从持“支持”态度的人中抽取了45人，求n的值；
    （Ⅱ）接受调查的人同时要对这项活动进行打分，其中6人打出的分数如下：9.2，9.6，8.7，9.3，9.0，8.2．把这6个人打出的分数看作一个总体，从中任取2个数，求该数与总体平均数之差的绝对值超过0.6的概率．

    查看答案和解析>>

    同步练习册答案