解:(1)当a=1时,函数f(x)=x-lnx,,x∈(0,+∞)
∵

,令f'(x)=0得x=(12分)
∵当x∈(0,1)时,f'(x)<0∴函数f(x)在(0,1)上为减函数
∵当x∈(1,+∞)时f'(x)>0∴函数f(x)在(1,+∞)上为增函数
∴当x=1时,函数f(x)有最小值,f(x)
最小值=f(1)=1(4分)
(2)∵

,
若a≤0,则对任意的x∈[1,+∞)都有f'(x)<0,∴函数f(x)在[1,+∞)上为减函数
∴函数f(x)在[1,+∞)上有最大值,没有最小值,f(x)
最大值=f(1)=a;(6分)
若a>0,令f'(x)=0得
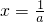
当0<a<1时,

,当
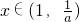
时f'(x)<0,函数f(x)在
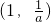
上为减函数
当
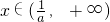
时f'(x)>0∴函数f(x)在
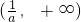
上为增函数
∴当
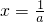
时,函数f(x)有最小值,
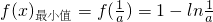
(8分)
当a≥1时,
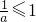
在[1,+∞)恒有f'(x)≥0
∴函数f(x)在[1,+∞)上为增函数,函数f(x)在[1,+∞)有最小值,f(x)
最小值=f(1)=a.(9分)
综上得:当a≤0时,函数f(x)在[1,+∞)上有最大值,f(x)
最大值=a;
当0<a<1时,函数f(x)有最小值,
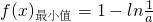
;
当a≥1时,函数f(x)在[1,+∞)有最小值,f(x)
最小值=a.(10分)
(3)证明:由(1)知函数f(x)=x-lnx在(0,+∞)上有最小值1
即对任意的x∈(0,+∞)都有x-lnx≥1,即x-1≥lnx,(12分)
当且仅当x=1时“=”成立
∵n∈N
*∴
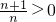
且
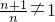
∴
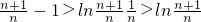
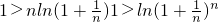
∴对任意的n∈N
*都有
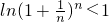
.(14分)
分析:(1)把a=1代入求出其导函数,得出其在定义域上的单调性即可求出函数f(x)的最值;
(2)先求出其导函数

,通过讨论a的取值得出函数在[1,+∞)上的单调性,进而求出函数f(x)在[1,+∞)上的最值;
(3)先由(1)知对任意的x∈(0,+∞)都有x-lnx≥1,即x-1≥lnx,再令x=

代入x-1≥lnx即可证明结论.
点评:本题主要考查利用导数求闭区间上函数的最值以及利用导数研究函数的单调性.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数和导数这一章最基本的知识,也是教学中的重点和难点.

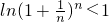 .
. ,令f'(x)=0得x=(12分)
,令f'(x)=0得x=(12分) ,
,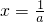
 ,当
,当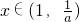 时f'(x)<0,函数f(x)在
时f'(x)<0,函数f(x)在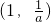 上为减函数
上为减函数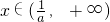 时f'(x)>0∴函数f(x)在
时f'(x)>0∴函数f(x)在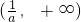 上为增函数
上为增函数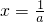 时,函数f(x)有最小值,
时,函数f(x)有最小值,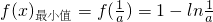 (8分)
(8分)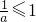 在[1,+∞)恒有f'(x)≥0
在[1,+∞)恒有f'(x)≥0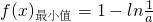 ;
;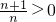 且
且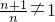
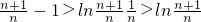
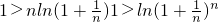
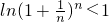 .(14分)
.(14分) ,通过讨论a的取值得出函数在[1,+∞)上的单调性,进而求出函数f(x)在[1,+∞)上的最值;
,通过讨论a的取值得出函数在[1,+∞)上的单调性,进而求出函数f(x)在[1,+∞)上的最值; 代入x-1≥lnx即可证明结论.
代入x-1≥lnx即可证明结论.
