
 如图,在长方形ABCD中,对角线BD与两邻边所成的角分别为α,β则cos2α+cos2β=1.仿此,在长方体ABCD-A′B′C′D′中,下列结论正确的是( )
如图,在长方形ABCD中,对角线BD与两邻边所成的角分别为α,β则cos2α+cos2β=1.仿此,在长方体ABCD-A′B′C′D′中,下列结论正确的是( )| A. | 若对角线BD′与面ABC,面ABB′,面BCB′所成的角为α,β,γ,则cos2α+cos2β+cos2γ=1 | |
| B. | 若对角线BD′与面ABC,面ABB′,面BCB′所成的角为α,β,γ,则cos2α+cos2β+cos2γ=2 | |
| C. | 若对角线BD′与三条棱AB,BC,BB′所成的角为α,β,γ,则cos2α+cos2β+cos2γ=2 | |
| D. | 以上类比结论均错误. |
分析 根据矩形的对角线BD与边BC和AB所成角分别为α,β,则cos2α+cos2β=1,推广到长方体ABCD-A′B′C′D′中,对角线BD′与面ABC,面ABB′,面BCB′所成的角分别为α、β、γ,得出cos2α+cos2β+cos2γ=2.
解答 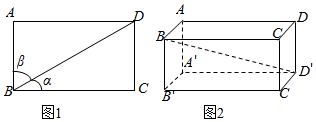 解:根据矩形的对角线BD与边AB和BC所成角分别为α,β,
解:根据矩形的对角线BD与边AB和BC所成角分别为α,β,
则cos2α+cos2β=cos2α+cos2($\frac{π}{2}$-α)=cos2α+sin2α=1,
把它推广到长方体ABCD-A′B′C′D′中,
对角线BD′与面ABC,面ABB′,面BCB′所成的角分别为α、β、γ,
则cos2α+cos2β+cos2γ=$\frac{{BD}^{2}}{{BD′}^{2}}$+$\frac{{BA′}^{2}}{{BD′}^{2}}$+$\frac{{BC′}^{2}}{{BD′}^{2}}$=$\frac{2{(AB}^{2}{+BC}^{2}{+BB′}^{2})}{{BD′}^{2}}$=$\frac{{2BD′}^{2}}{{BD′}^{2}}$=2.
故选:B.
点评 本题考查了类比推理的应用问题,也考查了直线与平面所成的角的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2016}{2017}$ | B. | $\frac{4032}{2017}$ | C. | $\frac{4034}{2018}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 4 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l⊥g,且l与圆相交 | B. | l⊥g,且l与圆相离 | C. | l∥g,且l与圆相交 | D. | l∥g,且l与圆相离 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com