【题目】
，
是两个平面，m，n是两条直线，有下列四个命题；
①如果
，
，
，那么
.
②如果，
，那么.
③如果
，
，那么
.
④如果
，，那么m与所成的角和n与所成的角相等.
其中正确的命题的个数为（ ）
A.1B.2C.3D.4
【答案】C
【解析】
对①，运用长方体模型，找出符合条件的直线和平面，即可判断；
对②，运用线面平行的性质定理和线面垂直的性质定理，即可判断；
对③，运用面面平行的性质定理，即可判断；
对④，由平行的传递性及线面角的定义，即可判断④．
对于命题①，可运用长方体举反例证明其错误：如图，
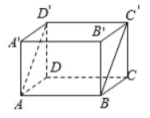
不妨设
为直线m，
为直线n，
所在的平面为
，
所在的平面为
，显然这些直线和平面满足题目条件，但
不成立；
命题②正确，证明如下：设过直线n的某平面与平面相交于直线l，则
，由
知
，从而
，结论正确；
由平面与平面平行的定义知命题如果
，
，那么
.③正确；
由平行的传递性及线面角的定义知命题：如果
，，那么m与所成的角和n与所成的角相等，④正确.
故选：C.
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案科目：高中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样
B.某地气象局预报：5月9日本地降水概率为
，结果这天没下雨，这表明天气预报并不科学
C.在回归分析模型中，残差平方和越小，说明模型的拟合效果越好
D.在回归直线方程
中，当解释变量
每增加1个单位时，预报变量
增加0.1个单位
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的方程为
，其焦点为
，
为过焦点的抛物线的弦，过
分别作抛物线的切线
，
，设，相交于点
．
（1）求
的值；
（2）如果圆
的方程为
，且点在圆内部，设直线与相交于
，
两点，求
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地某所高中2019年的高考考生人数是2016年高考考生人数的1.2倍，为了更好地对比该校考生的升学情况，统计了该校2016年和2019年的高考升学情况，得到如图所示：则下列结论正确的（ ）
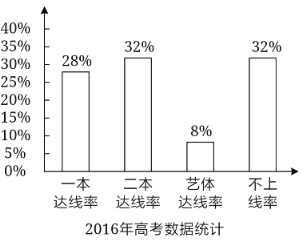
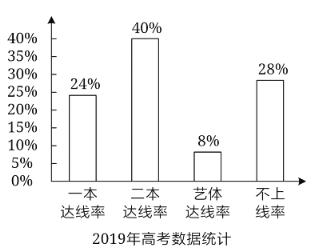
A.与2016年相比，2019年一本达线人数有所减少
B.与2016年相比，2019年二本达线人数增加了1倍
C.与2016年相比，2019年艺体达线人数相同
D.与2016年相比，2019年不上线的人数有所增加
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2019年4月，甲乙两校的学生参加了某考试机构举行的大联考，现对这两校参加考试的学生的数学成绩进行统计分析，数据统计显示，考生的数学成绩
服从正态分布
，从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷，并将这40份试卷的得分制作成如图所示的茎叶图：
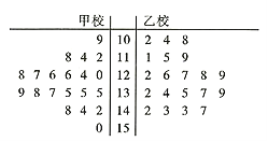
（1）试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数；
（2）若把数学成绩不低于135分的记作数学成绩优秀，根据茎叶图中的数据，判断是否有
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关？
（3）从所有参加此次联考的学生中（人数很多）任意抽取3人，记数学成绩在134分以上的人数为
，求的数学期望．
附：若随机变量服从正态分布
，则
，
，
．
参考公式与临界值表：
，其中
．
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
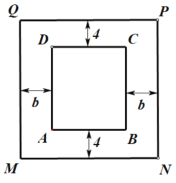
【题目】一酒企为扩大生产规模，决定新建一个底面为长方形
的室内发酵馆，发酵馆内有一个无盖长方体发酵池，其底面为长方形
(如图所示)，其中
.结合现有的生产规模，设定修建的发酵池容积为450米
，深2米.若池底和池壁每平方米的造价分别为200元和150元，发酵池造价总费用不超过65400元
（1）求发酵池
边长的范围；
（2）在建发酵馆时，发酵池的四周要分别留出两条宽为4米和
米的走道（为常数）.问:发酵池的边长如何设计，可使得发酵馆占地面积最小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如果一个实数数列
满足条件：
(
为常数，
，则这一数列为“伪等差数列”，称“伪公差”.给出下列关于某个伪等差数列的结论：其中正确的结论是__________________.
①对于任意的首项
，若
，则这一数列必为有穷数列；
②当
时，这一数列必为单调递増数列；
③这一数列可以是周期数列；
④若这一数列的首项为1，伪公差为3，
可以是这一数列中的一项.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
