
”¾ĢāÄæ”æŅ»¾ĘĘóĪŖĄ©“óÉś²ś¹ęÄ££¬¾ö¶ØŠĀ½ØŅ»øöµ×ĆęĪŖ³¤·½ŠĪ![]() µÄŹŅÄŚ·¢½Ķ¹Ż£¬·¢½Ķ¹ŻÄŚÓŠŅ»øöĪŽøĒ³¤·½Ģå·¢½Ķ³Ų£¬Ęäµ×ĆęĪŖ³¤·½ŠĪ
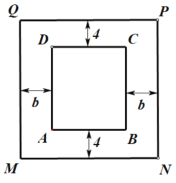
µÄŹŅÄŚ·¢½Ķ¹Ż£¬·¢½Ķ¹ŻÄŚÓŠŅ»øöĪŽøĒ³¤·½Ģå·¢½Ķ³Ų£¬Ęäµ×ĆęĪŖ³¤·½ŠĪ![]() (ČēĶ¼ĖłŹ¾)£¬ĘäÖŠ
(ČēĶ¼ĖłŹ¾)£¬ĘäÖŠ![]() .½įŗĻĻÖÓŠµÄÉś²ś¹ęÄ££¬Éč¶ØŠŽ½ØµÄ·¢½Ķ³ŲČŻ»żĪŖ450Ć×
.½įŗĻĻÖÓŠµÄÉś²ś¹ęÄ££¬Éč¶ØŠŽ½ØµÄ·¢½Ķ³ŲČŻ»żĪŖ450Ć×![]() £¬Éī2Ć×.Čō³Ųµ×ŗĶ³Ų±ŚĆæĘ½·½Ć×µÄŌģ¼Ū·Ö±šĪŖ200ŌŖŗĶ150ŌŖ£¬·¢½Ķ³ŲŌģ¼Ū×Ü·ŃÓĆ²»³¬¹ż65400ŌŖ
£¬Éī2Ć×.Čō³Ųµ×ŗĶ³Ų±ŚĆæĘ½·½Ć×µÄŌģ¼Ū·Ö±šĪŖ200ŌŖŗĶ150ŌŖ£¬·¢½Ķ³ŲŌģ¼Ū×Ü·ŃÓĆ²»³¬¹ż65400ŌŖ
£Ø1£©Ēó·¢½Ķ³Ų![]() ±ß³¤µÄ·¶Ī§£»
±ß³¤µÄ·¶Ī§£»
£Ø2£©ŌŚ½Ø·¢½Ķ¹ŻŹ±£¬·¢½Ķ³ŲµÄĖÄÖÜŅŖ·Ö±šĮō³öĮ½ĢõæķĪŖ4Ć×ŗĶ![]() Ć×µÄ×ßµĄ£Ø
Ć×µÄ×ßµĄ£Ø![]() ĪŖ³£Źż£©.ĪŹ:·¢½Ķ³ŲµÄ±ß³¤ČēŗĪÉč¼Ę£¬æÉŹ¹µĆ·¢½Ķ¹ŻÕ¼µŲĆ껿×īŠ”.
ĪŖ³£Źż£©.ĪŹ:·¢½Ķ³ŲµÄ±ß³¤ČēŗĪÉč¼Ę£¬æÉŹ¹µĆ·¢½Ķ¹ŻÕ¼µŲĆ껿×īŠ”.
”¾“š°ø”æ£Ø1£©![]() £Ø2£©µ±
£Ø2£©µ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬![]() Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»µ±
Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»µ±![]() Ź±£¬
Ź±£¬![]() Ź±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»µ±
Ź±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»µ±![]() Ź±£¬
Ź±£¬![]() Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”.
Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”.
”¾½āĪö”æ
£Ø1£©Éč![]() Ć×£¬×Ü·ŃÓĆĪŖ
Ć×£¬×Ü·ŃÓĆĪŖ![]() £¬½ā
£¬½ā![]() ¼“æÉµĆ½ā£»
¼“æÉµĆ½ā£»
£Ø2£©½įŗĻ£Ø1£©æɵĆÕ¼µŲĆ껿![]() ½įŗĻµ¼ŗÆŹż·ÖĄąĢÖĀŪ¼“æÉĒóµĆ×īÖµ.
½įŗĻµ¼ŗÆŹż·ÖĄąĢÖĀŪ¼“æÉĒóµĆ×īÖµ.
£Ø1£©ÓÉĢāŅāÖŖ:¾ŲŠĪ![]() Ć껿
Ć껿![]() Ć×
Ć×![]() £¬
£¬
Éč![]() Ć×£¬Ōņ
Ć×£¬Ōņ![]() Ć×£¬ÓÉĢāŅāÖŖ:
Ć×£¬ÓÉĢāŅāÖŖ:![]() £¬µĆ
£¬µĆ![]() £¬
£¬
Éč×Ü·ŃÓĆĪŖ![]() £¬
£¬
Ōņ![]() £¬
£¬
½āµĆ:![]() £¬ÓÖ
£¬ÓÖ![]() £¬¹Ź
£¬¹Ź![]() £¬
£¬
ĖłŅŌ·¢½Ķ³Ų![]() ±ß³¤µÄ·¶Ī§ŹĒ²»Š”ÓŚ15Ć×£¬ĒŅ²»³¬¹ż25Ć×£»
±ß³¤µÄ·¶Ī§ŹĒ²»Š”ÓŚ15Ć×£¬ĒŅ²»³¬¹ż25Ć×£»
£Ø2£©Éč·¢½Ķ¹ŻµÄÕ¼µŲĆ껿ĪŖ![]() ÓÉ£Ø1£©ÖŖ:
ÓÉ£Ø1£©ÖŖ:![]() £¬
£¬ ![]()
¢Ł![]() Ź±£¬
Ź±£¬![]() £¬
£¬![]() ŌŚ
ŌŚ![]() ÉĻµŻŌö£¬Ōņ
ÉĻµŻŌö£¬Ōņ![]() £¬¼“
£¬¼“![]() Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»
Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»
¢Ś![]() Ź±£¬
Ź±£¬![]() £¬
£¬![]() ŌŚ
ŌŚ![]() ÉĻµŻ¼õ£¬Ōņ
ÉĻµŻ¼õ£¬Ōņ![]() £¬¼“
£¬¼“![]() Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»
Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»
¢Ū![]() Ź±£¬
Ź±£¬![]() Ź±£¬
Ź±£¬![]() £¬
£¬![]() µŻ¼õ£»
µŻ¼õ£»![]() Ź±£¬
Ź±£¬![]() µŻŌö£¬
µŻŌö£¬
Ņņ“Ė![]() £¬¼“
£¬¼“![]() Ź±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»
Ź±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»
×ŪÉĻĖłŹö£ŗµ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬![]() Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»µ±
Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»µ±![]() Ź±£¬
Ź±£¬![]() Ź±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»µ±
Ź±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”£»µ±![]() Ź±£¬
Ź±£¬![]() Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”.
Ć׏±£¬·¢½Ķ¹ŻµÄÕ¼µŲĆ껿×īŠ”.


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ![]() Ę½Ćę
Ę½Ćę![]() £¬ĖıߊĪ
£¬ĖıߊĪ![]() ĪŖ¾ŲŠĪ£¬ĖıߊĪ
ĪŖ¾ŲŠĪ£¬ĖıߊĪ![]() ĪŖÖ±½ĒĢŻŠĪ£¬
ĪŖÖ±½ĒĢŻŠĪ£¬![]() £¬AB”ĪCD£¬
£¬AB”ĪCD£¬![]() £¬
£¬![]() £®
£®

£Ø1£©ĒóÖ¤£ŗ![]() Ę½Ćę
Ę½Ćę![]() £»
£»
£Ø2£©ĒóČżĄā׶![]() µÄĢå»ż£®
µÄĢå»ż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ![]() £¬
£¬![]() ŹĒĮ½øöĘ½Ćę£¬m£¬nŹĒĮ½ĢõÖ±Ļߣ¬ÓŠĻĀĮŠĖÄøöĆüĢā£»
ŹĒĮ½øöĘ½Ćę£¬m£¬nŹĒĮ½ĢõÖ±Ļߣ¬ÓŠĻĀĮŠĖÄøöĆüĢā£»
¢ŁČē¹ū![]() £¬
£¬![]() £¬
£¬![]() £¬ÄĒĆ“
£¬ÄĒĆ“![]() .
.
¢ŚČē¹ū![]() £¬
£¬![]() £¬ÄĒĆ“
£¬ÄĒĆ“![]() .
.
¢ŪČē¹ū![]() £¬
£¬![]() £¬ÄĒĆ“
£¬ÄĒĆ“![]() .
.
¢ÜČē¹ū![]() £¬
£¬![]() £¬ÄĒĆ“mÓė
£¬ÄĒĆ“mÓė![]() Ėł³ÉµÄ½ĒŗĶnÓė
Ėł³ÉµÄ½ĒŗĶnÓė![]() Ėł³ÉµÄ½ĒĻąµČ.
Ėł³ÉµÄ½ĒĻąµČ.
ĘäÖŠÕżČ·µÄĆüĢāµÄøöŹżĪŖ£Ø £©
A.1B.2C.3D.4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°ÖŠ¹śŹ£Óą¶ØĄķ”±ÓÖ³Ę”°Ėļ×Ó¶ØĄķ”±£¬×īŌēæɼūÓŚÖŠ¹śÄĻ±±³ÆŹ±ĘŚµÄŹżŃ§Öų×÷”¶Ėļ×ÓĖć¾”·¾ķĻĀµŚ¶žŹ®ĮłĢā£¬½Š×ö”°Īļ²»ÖŖŹż”±£¬ŌĪÄČēĻĀ£ŗ½ńÓŠĪļ²»ÖŖĘ䏿£¬ČżČżŹżÖ®Ź£¶ž£¬ĪåĪåŹżÖ®Ź£Čż£¬ĘßĘߏżÖ®Ź£¶ž.ĪŹĪļ¼øŗĪ£æĻÖÓŠÕāŃłŅ»øöĻą¹ŲµÄĪŹĢā£ŗ½«1µ½2020Õā2020øö×ŌČ»ŹżÖŠ±»5³żÓą3ĒŅ±»7³żÓą2µÄŹż°“ÕÕ“ÓŠ”µ½“óµÄĖ³ŠņÅųÉŅ»ĮŠ£¬¹¹³ÉŅ»øöŹżĮŠ£¬ŌņøĆŹżĮŠø÷ĻīÖ®ŗĶĪŖ£Ø £©
A.56383B.57171C.59189D.61242
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ä³ÉśĢ¬Ō°½«Ņ»Čż½ĒŠĪµŲæéABCµÄŅ»½ĒAPQæŖ±ŁĪŖĖ®¹ūŌ°ÖÖÖ²ĢŅŹ÷£¬ŅŃÖŖ½ĒAĪŖ![]() µÄ³¤¶Č¾ł“óÓŚ200Ć×£¬ĻÖŌŚ±ß½ēAP£¬AQ“¦½ØĪ§Ē½£¬ŌŚPQ“¦Ī§ÖńĄé°Ź.
µÄ³¤¶Č¾ł“óÓŚ200Ć×£¬ĻÖŌŚ±ß½ēAP£¬AQ“¦½ØĪ§Ē½£¬ŌŚPQ“¦Ī§ÖńĄé°Ź.
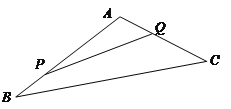
£Ø1£©ČōĪ§Ē½AP,AQ×ܳ¤¶ČĪŖ200Ć×£¬ČēŗĪĪ§æÉŹ¹µĆČż½ĒŠĪµŲæéAPQµÄĆ껿×ī“ó£æ
£Ø2£©ŅŃÖŖAP¶ĪĪ§Ē½øß1Ć×£¬AQ¶ĪĪ§Ē½øß1.5Ć×£¬Ōģ¼Ū¾łĪŖĆæĘ½·½Ć×100ŌŖ.ČōĪ§Ī§Ē½ÓĆĮĖ20000ŌŖ£¬ĪŹČēŗĪĪ§æÉŹ¹ÖńĄé°ŹÓĆĮĻ×īŹ”£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ĒśĻßCµÄ²ĪŹż·½³ĢĪŖ![]() £¬£Ø¦ČĪŖ²ĪŹż£©£¬ŅŌŌµćĪŖ¼«µć£¬xÖį·Ēøŗ°ėÖįĪŖ¼«Öį½ØĮ¢¼«×ų±źĻµ£®
£¬£Ø¦ČĪŖ²ĪŹż£©£¬ŅŌŌµćĪŖ¼«µć£¬xÖį·Ēøŗ°ėÖįĪŖ¼«Öį½ØĮ¢¼«×ų±źĻµ£®
£Ø1£©ĒóĒśĻßCµÄ¼«×ų±ź·½³Ģ£»
£Ø2£©ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬A£Ø©2£¬0£©£¬B£Ø0£¬©2£©£¬MŹĒĒśĻßCÉĻČĪŅāŅ»µć£¬Ēó”÷ABMĆ껿µÄ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ÆŌ²![]() ÓėŌ²
ÓėŌ²![]() £ŗ
£ŗ ![]() ĻąĒŠ£¬ĒŅÓėŌ²
ĻąĒŠ£¬ĒŅÓėŌ²![]() £ŗ
£ŗ ![]() ĻąÄŚĒŠ£¬¼ĒŌ²ŠÄ
ĻąÄŚĒŠ£¬¼ĒŌ²ŠÄ![]() µÄ¹ģ¼£ĪŖĒśĻß
µÄ¹ģ¼£ĪŖĒśĻß![]() .Éč
.Éč![]() ĪŖĒśĻß
ĪŖĒśĻß![]() ÉĻµÄŅ»øö²»ŌŚ
ÉĻµÄŅ»øö²»ŌŚ![]() ÖįÉĻµÄ¶Æµć£¬
ÖįÉĻµÄ¶Æµć£¬ ![]() ĪŖ×ų±źŌµć£¬¹żµć
ĪŖ×ų±źŌµć£¬¹żµć![]() ×÷
×÷![]() µÄĘ½ŠŠĻß½»ĒśĻß
µÄĘ½ŠŠĻß½»ĒśĻß![]() ÓŚ
ÓŚ![]() ,
, ![]() Į½øö²»Ķ¬µÄµć.
Į½øö²»Ķ¬µÄµć.
£Ø¢ń£©ĒóĒśĻß![]() µÄ·½³Ģ£»
µÄ·½³Ģ£»
£Ø¢ņ£©ŹŌĢ½¾æ![]() ŗĶ
ŗĶ![]() µÄ±ČÖµÄÜ·ńĪŖŅ»øö³£Źż£æČōÄÜ£¬Ēó³öÕāøö³£Źż£¬Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£»
µÄ±ČÖµÄÜ·ńĪŖŅ»øö³£Źż£æČōÄÜ£¬Ēó³öÕāøö³£Źż£¬Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø¢ó£©¼Ē![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £¬
£¬ ![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £¬Įī
£¬Įī![]() £¬Ēó
£¬Ēó![]() µÄ×ī“óÖµ.
µÄ×ī“óÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°ĀĢĖ®ĒąÉ½¾ĶŹĒ½šÉ½Ņųɽ”±µÄĄķÄīŌ½Ą“Ō½ÉīČėČĖŠÄ£¬¾Ż“Ė£¬Ä³ĶųÕ¾µ÷²éĮĖČĖĆĒ¶ŌÉśĢ¬ĪÄĆ÷½ØÉčµÄ¹Ų×¢Ēéæö£¬µ÷²éŹż¾Ż±ķĆ÷£¬²ĪÓėµ÷²éµÄČĖŌ±ÖŠ¹Ų×¢ÉśĢ¬ĪÄĆ÷½ØÉčµÄŌ¼Õ¼80%.ĻÖ“Ó²ĪÓėµ÷²éµÄ¹Ų×¢ÉśĢ¬ĪÄĆ÷½ØÉčµÄČĖŌ±ÖŠĖ껜є³ö200ČĖ£¬²¢½«Õā200ČĖ°“ÄźĮä£Øµ„Ī»£ŗĖź£©·Ö×é£ŗµŚ1×é[15£¬25£©£¬µŚ2×é[25£¬35£©£¬µŚ3×é[35£¬45£©£¬µŚ4×é[45£¬55£©£¬µŚ5×é[55£¬65]£¬µĆµ½µÄʵĀŹ·Ö²¼Ö±·½Ķ¼ČēĶ¼ĖłŹ¾.
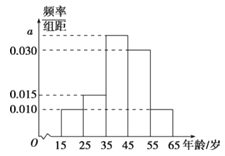
£Ø¢ń£©ĒóÕā200ČĖµÄĘ½¾łÄźĮä£ØĆæŅ»×éÓĆøĆ×éĒų¼äµÄÖŠµćÖµ×÷ĪŖ“ś±ķ£©ŗĶÄźĮäµÄÖŠĪ»Źż£Ø±£ĮōŅ»Ī»Š”Źż£©£»
£Ø¢ņ£©ĻÖŌŚŅŖ“ÓÄźĮäŌŚµŚ1£¬2×éµÄČĖŌ±ÖŠÓĆ·Ö²ć³éŃłµÄ·½·Ø³éČ”5ČĖ£¬ŌŁ“ÓÕā5ČĖÖŠĖ껜³éČ”3ČĖ½ųŠŠĪŹ¾ķµ÷²é£¬Ēó³éČ”µÄ3ČĖÖŠĒ”ÓŠ2ČĖµÄÄźĮäŌŚµŚ2×éÖŠµÄøÅĀŹ£»
£Ø¢ó£©Čō“ÓĖłÓŠ²ĪÓėµ÷²éµÄČĖ£ØČĖŹżŗܶą£©ÖŠČĪŅāŃ”³ö3ČĖ£¬ÉčÕā3ČĖÖŠ¹Ų×¢ÉśĢ¬ĪÄĆ÷½ØÉčµÄČĖŹżĪŖX£¬ĒóĖ껜±äĮæXµÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĪŅĆĒµÄ½Ģ²Ä±ŲŠŽŅ»ÖŠÓŠÕāŃłŅ»øöĪŹĢā£¬¼ŁÉčÄćÓŠŅ»±Ź×Ź½š£¬ĻÖÓŠČżÖÖĶ¶×Ź·½°ø¹©ÄćŃ”Ōń£¬ÕāČżÖÖ·½°øµÄ»Ų±ØČēĻĀ:
·½°øŅ»£ŗĆæĢģ»Ų±Ø![]() ŌŖ£»
ŌŖ£»
·½°ø¶ž£ŗµŚŅ»Ģģ»Ų±Ø![]() ŌŖ£¬ŅŌŗóĆæĢģ±ČĒ°Ņ»Ģģ¶ą»Ų±Ø
ŌŖ£¬ŅŌŗóĆæĢģ±ČĒ°Ņ»Ģģ¶ą»Ų±Ø![]() ŌŖ£»
ŌŖ£»
·½°øČż£ŗµŚŅ»Ģģ»Ų±Ø![]() ŌŖ£¬ŅŌŗóĆæĢģµÄ»Ų±Ø±ČĒ°Ņ»Ģģ·Ņ»·¬.
ŌŖ£¬ŅŌŗóĆæĢģµÄ»Ų±Ø±ČĒ°Ņ»Ģģ·Ņ»·¬.
¼ĒČżÖÖ·½°øµŚ![]() ĢģµÄ»Ų±Ø·Ö±šĪŖ
ĢģµÄ»Ų±Ø·Ö±šĪŖ![]() £¬
£¬![]() £¬
£¬![]() .
.
£Ø1£©øł¾ŻŹżĮŠµÄ¶ØŅåÅŠ¶ĻŹżĮŠ![]() £¬
£¬![]() £¬
£¬![]() µÄĄąŠĶ£¬²¢¾Ż“ĖŠ“³öČżøöŹżĮŠµÄĶØĻī¹«Ź½£»
µÄĄąŠĶ£¬²¢¾Ż“ĖŠ“³öČżøöŹżĮŠµÄĶØĻī¹«Ź½£»
£Ø2£©Š”Ķõ×¼±ø×öŅ»øöĪŖĘŚŹ®ĢģµÄ¶ĢĘŚĶ¶×Ź£¬ĖūÓ¦øĆŃ”ŌńÄÄŅ»ÖÖĶ¶×Ź·½°ø£æ²¢ĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com