
【题目】![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,已知
的中点,已知![]() ,
,![]() ,
,![]() .
.
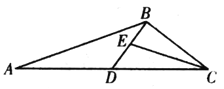
(1)求角![]() 的大小和
的大小和![]() 的长;
的长;
(2)设![]() 的角平分线交
的角平分线交![]() 于
于![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由三角函数恒等变换的应用化简已知等式可得tanC![]() ,结合范围C∈(0,π),可求C的值,由余弦定理可得BD的值.
,结合范围C∈(0,π),可求C的值,由余弦定理可得BD的值.
(2)由(1)可知BD2+BC2=4=CD2,可求∠DBC![]() ,可得S△DBC
,可得S△DBC![]() ,利用三角形的面积公式可求S△BCE
,利用三角形的面积公式可求S△BCE![]() S△CED,代入S△BCE+S△CED=S△BCD
S△CED,代入S△BCE+S△CED=S△BCD![]() ,即可解得S△CED的值.
,即可解得S△CED的值.
(1)∵由题意可得:![]() sinC+1﹣2sin2
sinC+1﹣2sin2![]() 0,
0,
∴![]() sinC+cos(A+B)=0,
sinC+cos(A+B)=0,
又A+B=π﹣C,
∴![]() sinC﹣cosC=0,可得tanC
sinC﹣cosC=0,可得tanC![]() ,
,
∵C∈(0,π),
∴C![]() ,
,
∴在△BCD中,由余弦定理可得:BD2=3+4﹣2![]() 1,
1,
解得:BD=1,
(2)由(1)可知BD2+BC2=4=CD2,
∴∠DBC![]() ,
,
∴S△DBC![]() BDBC
BDBC![]() ,
,
∵CE是∠BCD的角平分线,
∴∠BCE=∠DCE,
在△CEB和△CED中,S△BCE![]() ,
,
S△CED![]() ,
,
可得:![]() ,
,
∴S△BCE![]() S△CED,
S△CED,
∴代入S△BCE+S△CED=S△BCD![]() ,(1
,(1![]() )S△CED
)S△CED![]() ,
,
∴S△CED![]() (2
(2![]() )=2
)=2![]() 3.
3.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.“![]() 为真”是“
为真”是“![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
B.若数据![]() 的平均数为1,则
的平均数为1,则![]() 的平均数为2;
的平均数为2;
C.在区间![]() 上随机取一个数
上随机取一个数![]() ,则事件“
,则事件“![]() ”发生的概率为
”发生的概率为![]()
D.设从总体中抽取的样本为![]() 若记样本横、纵坐标的平均数分别为
若记样本横、纵坐标的平均数分别为![]() ,则回归直线
,则回归直线![]() 必过点
必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() 是两个平面,m,n是两条直线,有下列四个命题;
是两个平面,m,n是两条直线,有下列四个命题;
①如果![]() ,
,![]() ,
,![]() ,那么
,那么![]() .
.
②如果![]() ,
,![]() ,那么
,那么![]() .
.
③如果![]() ,
,![]() ,那么
,那么![]() .
.
④如果![]() ,
,![]() ,那么m与
,那么m与![]() 所成的角和n与
所成的角和n与![]() 所成的角相等.
所成的角相等.
其中正确的命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为![]() 的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
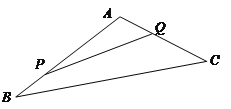
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com