
【题目】我们把离心率e= ![]() 的双曲线
的双曲线 ![]() =1(a>0,b>0)称为黄金双曲线.如图是双曲线
=1(a>0,b>0)称为黄金双曲线.如图是双曲线 ![]() =1(a>0,b>0,c=
=1(a>0,b>0,c= ![]() )的图象,给出以下几个说法: ①若b2=ac,则该双曲线是黄金双曲线;
)的图象,给出以下几个说法: ①若b2=ac,则该双曲线是黄金双曲线;
②若F1 , F2为左右焦点,A1 , A2为左右顶点,B1(0,b),B2(0,﹣b)且∠F1B1A2=90°,则该双曲线是黄金双曲线;
③若MN经过右焦点F2且MN⊥F1F2 , ∠MON=90°,则该双曲线是黄金双曲线.
其中正确命题的序号为 . 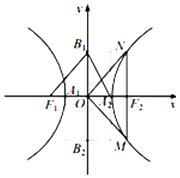
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sin(2x+
=(sin(2x+ ![]() ),sinx),
),sinx), ![]() =(1,sinx),f(x)=
=(1,sinx),f(x)= ![]() .
.
(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,a=2 ![]() ,
, ![]() ,若
,若 ![]() sin(A+C)=2cosC,求b的大小.
sin(A+C)=2cosC,求b的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B两点分别在两条互相垂直的直线y=2x和x+ay=0上,且线段AB的中点为P(0, ![]() ),则直线AB的方程为( )
),则直线AB的方程为( )
A.y=- ![]() x+5
x+5
B.y= ![]() x-5
x-5
C.y= ![]() x+5
x+5
D.y=- ![]() x-5
x-5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1中,如图E、F分别是BB1 , CD的中点, 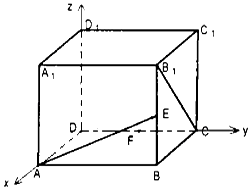
(1)求证:D1F⊥AE;
(2)求直线EF与CB1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图. 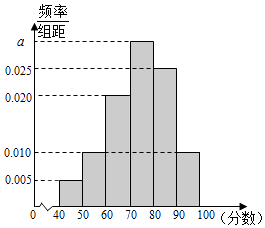
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a , b的值.
(1)l1⊥l2 , 且l1过点(1,1);
(2)l1∥l2 , 且l2在第一象限内与两坐标轴围成的三角形的面积为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=5sin3x+5 ![]() cos3x,下列说法正确的是( )
cos3x,下列说法正确的是( )
A.函数f(x)关于x= ![]() π对称
π对称
B.函数f(x)向左平移 ![]() 个单位后是奇函数
个单位后是奇函数
C.函数f(x)关于点( ![]() ,0)中心对称
,0)中心对称
D.函数f(x)在区间[0, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,利用简单随机抽样的方法在全校一年级学生中进行了抽样调查,调查结果如表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)根据(1)的结论,你能否提出更好的调查方法来了解该校大学新生的饮食习惯,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com