
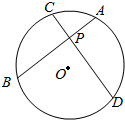
 如图,某工业园区是半径为10km的圆形区域,距离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.
如图,某工业园区是半径为10km的圆形区域,距离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.分析 (1)连结OA,OB,利用余弦定理求出AB,根据圆的性质求出AB的最值,列出不等式求出α的范围;使用作差法求出弓形的面积;
(2)过O分别作AB,CD的垂线段OE,OF,设AB=x,根据勾股定理和垂径定理求出CD,AB+CD是关于x的函数,利用导数求出该函数的最小值.
解答 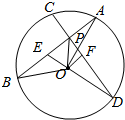 解:(1)连结OA,OB,则∠AOB=α,OA=OB=10,在△AOB中,由余弦定理得AB=$\sqrt{O{A}^{2}+O{B}^{2}-2OA•OBcosα}$=$\sqrt{200-200cosα}$.
解:(1)连结OA,OB,则∠AOB=α,OA=OB=10,在△AOB中,由余弦定理得AB=$\sqrt{O{A}^{2}+O{B}^{2}-2OA•OBcosα}$=$\sqrt{200-200cosα}$.
∵OP=5,∴当OP⊥AB时,AB取得最小值2$\sqrt{1{0}^{2}-{5}^{2}}$=10$\sqrt{3}$,当AB过圆心O时,AB取得最大值20,
∴10$\sqrt{3}$≤$\sqrt{200-200cosα}$≤20,解得-1≤cosα≤-$\frac{1}{2}$.∴$\frac{2π}{3}$≤α≤π.∴α的最小值为$\frac{2π}{3}$.
较小区域面积S(α)=S扇形OAB-S△AOB=$\frac{α}{2π}•πO{A}^{2}$-$\frac{1}{2}O{A}^{2}•sinα$=50α-50sinα.∴S′(α)=50-50cosα>0,
∴S(α)在[$\frac{2π}{3}$,π]上是增函数,∴Smin(α)=S($\frac{2π}{3}$)=$\frac{100π}{3}$-25$\sqrt{3}$(km2).
(2)过O分别作AB,CD的垂线段OE,OF,则四边形OEPF是矩形,AE=$\frac{AB}{2}$,DF=$\frac{CD}{2}$,设AB=x,则OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{100-\frac{{x}^{2}}{4}}$,
∴OF=PE=$\sqrt{O{P}^{2}-O{E}^{2}}$=$\sqrt{\frac{{x}^{2}}{4}-75}$,∴DF=$\sqrt{O{D}^{2}-O{F}^{2}}$=$\sqrt{175-\frac{{x}^{2}}{4}}$,∴CD=2DF=2$\sqrt{175-\frac{{x}^{2}}{4}}$=$\sqrt{700-{x}^{2}}$.
∴AB+CD=x+$\sqrt{700-{x}^{2}}$.∴(AB+CD)2=700+2x$\sqrt{700-{x}^{2}}$=700+2$\sqrt{700{x}^{2}-{x}^{4}}$.
令f(x)=700x2-x4,则f′(x)=1400x-4x3,令f′(x)=0得x=0(舍)或x=$\sqrt{350}$或x=-$\sqrt{350}$(舍).
当10$\sqrt{3}$≤x<$\sqrt{350}$时,f′(x)>0,当$\sqrt{350}$<x≤20时,f′(x)<0.
∴f(x)在[10$\sqrt{3}$,$\sqrt{350}$]上是增函数,在[$\sqrt{350}$,20]上是减函数.
∵f(10$\sqrt{3}$)=120000,f(20)=120000,∴f(x)的最小值为120000.
∴(AB+CD)2的最小值是700+2$\sqrt{120000}$=700+400$\sqrt{3}$=(10$\sqrt{3}$+20)2,∴AB+CD的最小值是10$\sqrt{3}$+20(km).
点评 本题考查了余弦定理,导数与函数的最值问题,在圆中常使用垂径定理来解决计算问题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤1 | B. | a≥1 | C. | a≤2 | D. | a≥2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com