
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由题意知f(x)=ex⊕1=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{1,x<0}\end{array}\right.$,从而依次对四个命题判断:
①举例a=0时即可,
②以ab的取值分类讨论,从而证明;
③举例a=b=-$\sqrt{ln2}$时即可,
④以a+b的取值分类讨论,从而证明.
解答 解:由题意知,
f(x)=ex⊕1=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{1,x<0}\end{array}\right.$,
①当a=0时,f(a)•f(-a)=1,故成立;
②当ab=0时,f(ab)=1,f(a2)≥1,f(b2)≥1,
故f(a2)+f(b2)≥2f(ab);
当ab<0时,f(ab)=1,f(a2)>1,f(b2)>1,
故f(a2)+f(b2)≥2f(ab);
当ab>0时,f(ab)=eab,f(a2)=${e}^{{a}^{2}}$,f(b2)=${e}^{{b}^{2}}$,
故f(a2)+f(b2)=${e}^{{a}^{2}}$+${e}^{{b}^{2}}$
≥2$\sqrt{{e}^{{a}^{2}}{e}^{{b}^{2}}}$=2$\sqrt{{e}^{{a}^{2}+{b}^{2}}}$
=2$\sqrt{{e}^{2ab}}$=2f(ab);
故对任意a,b∈R,都有f(a2)+f(b2)≥2f(ab),故成立;
③当a=b=-$\sqrt{ln2}$时,
f(a)+f(b)=2=f(ab)=2,故成立;
④当a+b≤0时,f(a+b)=1,
故f(a)•f(b)≥f(a+b);
当a+b>0时,
若ab≥0,f(a)•f(b)=ea•eb=ea+b=f(a+b),
若ab<0,则不妨设a<0,
则f(a)•f(b)=eb>ea+b=f(a+b);
故对任意a,b∈R,都有f(a)•f(b)≥f(a+b),故成立.
故选:D.
点评 本题考查了分段函数的应用及基本不等式的应用,同时考查了分类讨论的思想应用.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [3,+∞) | C. | (-∞,-1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{1+x}$ | B. | -$\frac{1}{1+x}$ | C. | $\frac{1}{(1+x)^{2}}$ | D. | -$\frac{1}{(1+x)^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
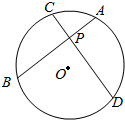 如图,某工业园区是半径为10km的圆形区域,距离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.
如图,某工业园区是半径为10km的圆形区域,距离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com