
| A. | a≤1 | B. | a≥1 | C. | a≤2 | D. | a≥2 |
分析 由?x1∈[-1,2],都?x2∈[1,2],使得f(x1)≥g(x2),可得f(x)=x2+1在x1∈[-1,2]的最小值不小于g(x)=ax+2在x2∈[1,2]的最小值,构造关于a的不等式组,可得结论.
解答 解:当x1∈[$\frac{1}{2}$,1]时,由f(x)=x+$\frac{4}{x}$得,f′(x)=$\frac{{x}^{2}-4}{{x}^{2}}$,
令f′(x)>0,解得:x>2,令f′(x)<0,解得:x<2,
∴f(x)在[$\frac{1}{2}$,1]单调递减,
∴f(1)=5是函数的最小值,
当x2∈[2,3]时,g(x)=2x+a为增函数,
∴g(2)=a+4是函数的最小值,
又∵?x1∈[$\frac{1}{2}$,1],都?x2∈[2,3],使得f(x1)≥g(x2),
可得f(x)在x1∈[$\frac{1}{2}$,1]的最小值不小于g(x)在x2∈[2,3]的最小值,
即5≥a+4,解得:a≤1,
故选:A.
点评 本题考查的知识是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
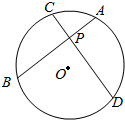 如图,某工业园区是半径为10km的圆形区域,距离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.
如图,某工业园区是半径为10km的圆形区域,距离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(2x-$\frac{π}{2}$) | B. | y=cos(2x-$\frac{π}{2}$) | C. | y=10x+10-x | D. | y=ln(x2+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com