
分析 (1)先求极差,再定组距,分组,统计频数,计算出各组的频率,列出频率分布表.
(2)以频率/组距为纵坐标,组距为横坐标作图出频率分布直方图.
解答 解:(1)最低身高151,最高身高180,确定组距为3,作频率分布表如下:
| 身高( ) | 频数 | 频率(%) |
| 150.5~153.5 | 2 | 4 |
| 153.5~156.5 | 2 | 4 |
| 156.5~159.5 | 5 | 10.0 |
| 159.5~162.5 | 6 | 12.0 |
| 162.5~165.5 | 9 | 18.0 |
| 165.5~168.5 | 12 | 24 |
| 168.5~171.5 | 6 | 12.0 |
| 171.5~174.5 | 3 | 6.0 |
| 174.5~177.5 | 2 | 4 |
| 177.5~180.5 | 3 | 4 |
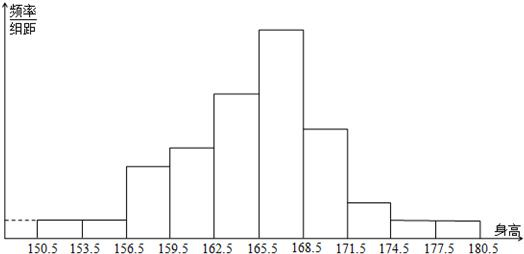
点评 本题考查频率分布直方图的作法,频率分布直方图是一个比较重要的考点,这几年的高考中多有体现.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | bc<ad | B. | bc>ad | C. | $\frac{a}{c}$$<\frac{1}{b}$ | D. | $\frac{a}{c}$$<\frac{b}{d}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
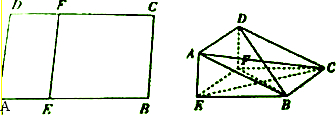
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com