
分析 由题意,D是BC上的点,DA=DB=2,DC=1,设AB=m,AC=n,根据余弦定理建立关系,利用基本不等式的性质求解.
解答 解:△ABC中,D是BC上的点,DA=DB=2,DC=1,设AB=m,AC=n,
cos∠BDA=$\frac{8-{m}^{2}}{8}$,cos∠CDA=$\frac{5-{n}^{2}}{4}$,
∠BDA与∠CDA互补,
∴$\frac{8-{m}^{2}}{8}$=-$\frac{5-{n}^{2}}{4}$,
可得:2n2+m2=18.
那么:AB•AC=m•n=$\frac{1}{\sqrt{2}}m•\sqrt{2}n$≤$\frac{1}{\sqrt{2}}$×$\frac{2{n}^{2}+{m}^{2}}{2}$=$\frac{9\sqrt{2}}{2}$(当且仅当m=$\sqrt{2}n$取等号)
故答案为$\frac{9\sqrt{2}}{2}$.
点评 本题考查了余弦定理的综合运用和基本不等式的性质的求解最值的问题.属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -32 | B. | -16 | C. | 32 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:| 等级 | 不合格 | 合格 | ||
| 得分 | [20,40) | [40,60) | [60,80) | [80,100] |
| 频数 | 6 | a | 24 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
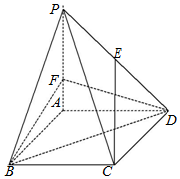 如图,在四棱锥P-ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com