Question

19．为了解学生寒假期间学习情况，学校对某班男、女学生学习时间进行调查，学习时间按整小时统计，调查结果绘成折线图如下：

（Ⅰ）已知该校有400名学生，试估计全校学生中，每天学习不足4小时的人数；
（Ⅱ）若从学习时间不少于4小时的学生中选取4人，设选到的男生人数为X，求随机变量X的分布列；
（Ⅲ）试比较男生学习时间的方差${S_1}^2$与女生学习时间方差$S_2^2$的大小．（只需写出结论）

Answer 1

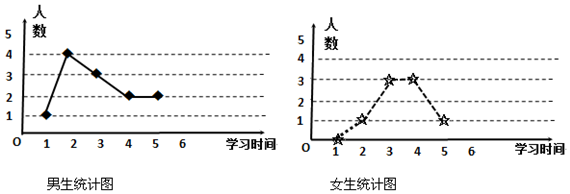
分析 （Ⅰ）根据题意，由折线图分析可得20名学生中有12名学生每天学习不足4小时，进而可以估计校400名学生中天学习不足4小时的人数；
（Ⅱ）学习时间不少于4本的学生共8人，其中男学生人数为4人，故X的取值为0，1，2，3，4；由古典概型公式计算可得X=0，1，2，3，4的概率，进而可得随机变量X的分布列；
（Ⅲ）根据题意，分析折线图，求出男生、女生的学习时间方差，比较可得答案．

解答 解：（Ⅰ）根据题意，由折线图可得12名男生中有8名每天学习不足4小时，
8名女生中有4名每天学习不足4小时，
即20名学生中有12名学生每天学习不足4小时，
每天学习不足4小时的人数为：$400×\frac{12}{20}=240$人．
（Ⅱ）学习时间不少于4本的学生共8人，其中男学生人数为4人，故X的取值为0，1，2，3，4．
由题意可得$P（X=0）=\frac{C_4^4}{C_8^4}=\frac{1}{70}$；   
 $P（X=1）=\frac{C_4^1C_4^3}{C_8^4}=\frac{16}{70}=\frac{8}{35}$；
$P（X=2）=\frac{C_4^2C_4^2}{C_8^4}=\frac{36}{70}=\frac{18}{35}$；  
  $P（X=3）=\frac{C_4^3C_4^1}{C_8^4}=\frac{16}{70}=\frac{8}{35}$；
$P（X=4）=\frac{C_4^4}{C_8^4}=\frac{1}{70}$．
所以随机变量X的分布列为

X	0	1	2	3	4
P	$\frac{1}{70}$	$\frac{8}{35}$	$\frac{18}{35}$	$\frac{8}{35}$	$\frac{1}{70}$

随机变量X的均值$EX=0×\frac{1}{70}+1×\frac{16}{70}+2×\frac{36}{70}+3×\frac{16}{70}+4×\frac{1}{70}=2$．
（Ⅲ）根据题意，对于男生，学习时间1小时的有1人，学习时间2小时的有4人，学习时间3小时的有3人，学习时间4小时的有2人，学习时间5小时的有2人，
其平均数${\overline{x}}_{1}$=$\frac{1}{12}$（1×1+2×4+3×3+4×2+5×2）=3，
其方差${s_1}^2$=$\frac{1}{12}$[（1-3）²+4×（2-3）²+3×（3-3）²+2×（4-3）²+2×（5-3）²]=1.5；
对于女生，学习时间2小时的有1人，学习时间3小时的有3人，学习时间4小时的有3人，学习时间5小时的有1人，
其平均数${\overline{x}}_{2}$=$\frac{1}{8}$（1×2+3×3+4×3+5×1）=3.5，
其方差${s_2}^2$=$\frac{1}{8}$[（2-3.5）²+3×（3-3.5）²+3×（4-3.5）²+（5-3.5）²]=0.75；
比较可得${s_1}^2＞$${s_2}^2$．

点评 本题考查随机变量的分布列、期望与方差的计算，涉及折线图的应用，关键是利用折线图分析数据．