练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为了庆祝第一个农民丰收节，西部山区某村统计了自2011年以来每年的年总收入，其中2018年统计的是1月到8月的总收入，统计结果如图所示.根据图形，下列四个判断中，错误的是（ ）

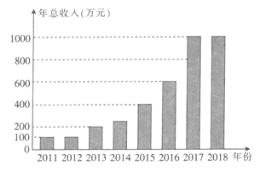
    A.从2012年起，年总收入逐年增加B.2017年的年总收入在2016年的基础上翻了番

    C.年份数与年总收入成正相关D.由图可预测从2014年起年总收入增长加快

    【答案】B

    【解析】

    根据条形图，对选项逐一分析，由此确定判断错误的选项.

    从图形可以看出，从2012年起，年总收入逐年增加，A是正确的；年份数与年总收入成正相关，C是正确的；从2014年起总收入增长加快，D是正确的；2017年的年总收入比2016年增加了万元，并没有翻一番，所以选项B是错误的.

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，多面体，平面平面，，，，是的中点，是上的点.

    （Ⅰ）若平面，证明：是的中点；

    （Ⅱ）若，，求二面角的平面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为坐标原点，点和点，动点满足：.

    （1）求动点的轨迹曲线的方程并说明是何种曲线；

    （2）若抛物线：的焦点恰为曲线的顶点，过点的直线与抛物线交于，两点，，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】谢宾斯基三角形是一种分形，由波兰数学家谢宾斯基在1915年提出，先作一个正三角形．挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用白色代表挖去的面积，那么黑三角形为剩下的面积（我们称黑三角形为谢宾斯基三角形）．向图中第5个大正三角形中随机撒512粒大小均匀的细小颗粒物，则落在白色区域的细小颗粒物的数量约是（ ）

    A.256B.350C.162D.96

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的右焦点为点的坐标为，为坐标原点，是等腰直角三角形.

    （1）求椭圆的方程；

    （2）经过点作直线交椭圆于两点，求面积的最大值；

    （3）是否存在直线交椭圆于两点，使点为的垂心（垂心：三角形三边高线的交点）？若存在，求出直线的方程；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆的右焦点为，以原点为圆心，短半轴长为半径的圆恰好经过椭圆的两焦点，且该圆截直线所得的弦长为.

    （1）求椭圆的标准方程；

    （2）过定点的直线交椭圆于两点、，椭圆上的点满足，试求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时.

    ①求函数在处的切线方程；

    ②定义其中，求；

    （2）当时，设，(为自然对数的底数)，若对任意给定的，在上总存在两个不同的，使得成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

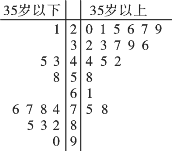
    【题目】某单位对其名员工的饮食习惯进行了一次调查，并用如图所示的茎叶图表示他们的饮食指数（说明：图中饮食指数低于的人，喜食蔬菜；饮食指数高于的人，喜食肉类）.

    （1）根据所给数据完成下面的列联表；

    喜食蔬菜

    喜食肉类

    总计

    35岁以上

    35岁以下

    总计

    （2）能否有的把握认为该单位员工的饮食习惯与年龄有关？

    独立性检验的临界值表：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    参考公式：，.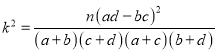

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 已知参赛号码为1~4号的四名射箭运动员参加射箭比赛。

    （1）通过抽签将他们安排到1~4号靶位，试求恰有一名运动员所抽靶位号与其参赛号码相同的概率；

    （2）记1号，2号射箭运动员，射箭的环数为（所有取值为0，1，2，3．．．，10）。

    根据教练员提供的资料，其概率分布如下表：

    0

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    0

    0

    0

    0

    0.06

    0.04

    0.06

    0.3

    0.2

    0.3

    0.04

    0

    0

    0

    0

    0.04

    0.05

    0.05

    0.2

    0.32

    0.32

    0.02

    1. 若1，2号运动员各射箭一次，求两人中至少有一人命中8环的概率；
    2. 判断1号，2号射箭运动员谁射箭的水平高？并说明理由．

    查看答案和解析>>

    同步练习册答案