考点:数列与不等式的综合,等差数列的前n项和,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)设等差数列{a
n}的首项为a
1,公差为d,利用a
2=5,S
5=55求出首项与公差,即可求解a
n及S
n;
(Ⅱ)化简
,利用裂项法求出前n项和T
n,通过判断前n项和T
n的单调性,求出最小值即可证明结果.
解答:
解:(Ⅰ)设等差数列{a
n}的首项为a
1,公差为d,
∵a
2=5,S
9=99,∴
99==9a5,得a
5=11
∴3d=a
5-a
2=6,∴d=2,a
1=3-------------------------------------(4分)
∴a
n=2n+1-------------------------------------(6分)
(Ⅱ)
bn====-------------------------------(9分)
∴
Tn=b1+b2+…+bn=(1-)+(-)+…+(-)=
1-<1------------(11分)
又因为
Tn+1-Tn=>0,所以
Tn>Tn-1>…>T1=所以
≤Tn<1------------------------------------------------(12分)
点评:本题考查数列求和,等差数列的应用,数列的函数的特征,数列与不等式的关系,是中档题.



 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案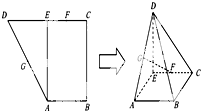 如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.
如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.