
分析 (1)根据奇函数的性质即可求出a的值,
(2)根据对数函数的性质,并注意对数函数的定义域,
(3)利用反证法证明即可.
解答 解(1)因为f(x)为其定义域内奇函数,
所以 f(x)+f(-x)=0,
即 $f(x)+f(-x)={log_3}\frac{1+x}{a-x}+{log_3}\frac{1-x}{a+x}=0$….….…..….(2分)
即 ${log_3}\frac{{1-{x^2}}}{{{a^2}-{x^2}}}=0⇒\frac{{1-{x^2}}}{{{a^2}-{x^2}}}=1$…..….(4分)
所以 1-x2=a2-x2⇒a=±1….…(5分)
当a=-1时,对数无意义,故舍去,
所以a=1…6分
(2)$f(x)={log_3}\frac{1+x}{1-x}$的定义域为(-1,1)…(7分)
由f(x)>1,得${log_3}\frac{1+x}{1-x}>1={log_3}3$,
∴$\frac{1+x}{1-x}>3⇒x>\frac{1}{2}$….….(9分)
又因为f(x)的定义域为(-1,1)
所以f(x)>1得解集为$(\frac{1}{2},1)$…(10分)
(3)证明:$f(\frac{1}{3})={log_3}2$(log32>0)…..….(11分)
假设log32为有理数,则其可以写成最简分数形式,而且唯一的,
设${log_3}2=\frac{n}{m}$(其中m,n为两个互质的正整数)….…(13分)
得 ${3^{\frac{n}{m}}}=2$,即3n=2m(*),
因为m,n为两个互质的正整数,
所以3m为奇数,2n为偶数,显然奇数不等于偶数,
所以(*)式不成立…(15分)
所以假设不成立,
所以$f(\frac{1}{3})={log_3}2$为无理数…(16分)
点评 本题考查奇函数的性质不等式的解法,和反证法,考查了学生的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+a | C. | 1+a+a2 | D. | 1+a+a2+a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{78}{71}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知双曲线C的方程记为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),点P($\sqrt{3}$,0)在双曲线上.离心率为e=2.
已知双曲线C的方程记为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),点P($\sqrt{3}$,0)在双曲线上.离心率为e=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
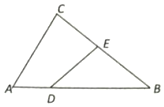 如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.
如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和④ | B. | ①和③ | C. | ③和④ | D. | ①和② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com