
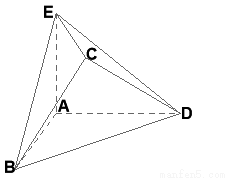
在几何体ABCDE中,AB=AD=BC=CD=2,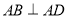 ,且
,且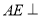 平面
平面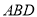 ,平面
,平面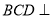 平面
平面 .
.
(1)当 平面
平面 时,求
时,求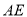 的长;
的长;
(2)当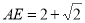 时,求二面角
时,求二面角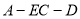 的大小.
的大小.
(1) ;(2)
;(2)
【解析】
试题分析:(1)设AE=a,如图建立空间直角坐标系,则A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,a),取BD中点T,连CT,AT,求出平面CDE的一个法向量为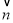 ,根据AB||平面CDE可得
,根据AB||平面CDE可得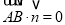 由此可求出a值,即AE长;(2)转化为求两平面法向量的夹角,由(1)易知平面CDE的一个法向量
由此可求出a值,即AE长;(2)转化为求两平面法向量的夹角,由(1)易知平面CDE的一个法向量 ,可证平面AEC的一个法向量
,可证平面AEC的一个法向量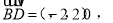 利用向量夹角公式即可求得,注意二面角与向量夹角的关系;
利用向量夹角公式即可求得,注意二面角与向量夹角的关系;
试题解析:(1)设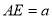 ,如图,建立空间直角坐标系,
,如图,建立空间直角坐标系,
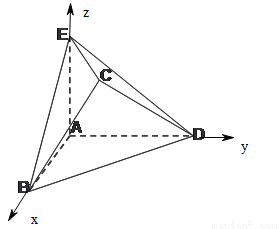
则A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,a),
取BD的中点T,连接CT,AT,则CT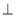 BD.
BD.
又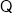 平面BCD
平面BCD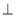 平面ABD,
平面ABD,
所以CT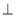 平面BCD,
平面BCD,
所以CT//AE.
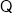 AB=AD=BC=CD=2,
AB=AD=BC=CD=2, ,
,
所以CD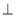 CB,
CB,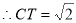 ,
,
 C(1,1,
C(1,1, ),
),

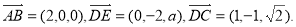
设平面CDE的法向量为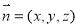 ,
,
则有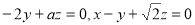 ,
, 
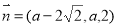 .
.
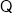 AB//平面CDE,
AB//平面CDE,

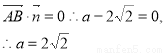
即AE的长为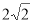 .
.
(2)连接AC,当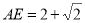 时,由(1)可知平面CDE的一个法向量
时,由(1)可知平面CDE的一个法向量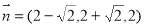 ,
,
又BD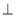 AT,BD
AT,BD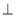 AE,
AE, BD
BD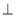 平面ACE,
平面ACE,
 平面ACE的一个法向量
平面ACE的一个法向量

 二面角
二面角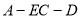 的大小为
的大小为 .
.
考点:二面角及其求法,空间向量求平面夹角


科目:高中数学 来源:2014-2015学年湖北省毕业生二月调研考试理科数学试卷(解析版) 题型:选择题
设椭圆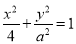 和双曲线
和双曲线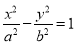 有共同的焦点,连接椭圆的焦点和短轴的一个端点所得直线和双曲线的一条渐近线平行,设双曲线的离心率为
有共同的焦点,连接椭圆的焦点和短轴的一个端点所得直线和双曲线的一条渐近线平行,设双曲线的离心率为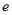 ,则
,则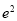 等于( )
等于( )
A. B.
B.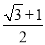
C.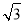 D.
D.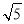
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省毕业生二月调研考试理科数学试卷(解析版) 题型:选择题
某班 名学生负责校内
名学生负责校内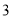 个不同地段的卫生工作,每个地段至少有
个不同地段的卫生工作,每个地段至少有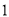 名学生的分配方案共有( )
名学生的分配方案共有( )
A.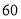 种 B.
种 B.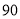 种 C.
种 C.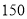 种 D.
种 D.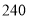 种
种
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省绥化市高三下学期期初开学联考理科数学试卷(解析版) 题型:选择题
设函数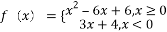 ,若互不相等的实数
,若互不相等的实数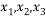 满足
满足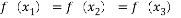 ,则
,则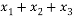 的取值范围是( )
的取值范围是( )
A.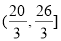 B.
B.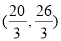 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com