
分析 (1)运用奇函数的定义,设x>0,则-x<0,结合f(-x)=-f(x),又f(0)=0,即可得到所求解析式;
(2)由题意可得f(x)=x2+mx+1(x>0)的图象与x轴正半轴有两个不同的交点,运用判别式和韦达定理,解不等式即可得到所求范围.
解答 解:(1)设x>0,则-x<0,∴f(-x)=-x2-mx-1┉┉┉┉┉┉┉┉┉┉(2分)
又f(x)为奇函数,即f(-x)=-f(x),所以,f(x)=x2+mx+1(x>0),(4分)
又f(0)=0,┉┉┉┉┉┉┉┉┉┉┉┉(6分)
所以$f(x)=\left\{\begin{array}{l}{x^2}+mx+1,\;x>0\\ 0\;,\;x=0\\-{x^2}+mx-1\;,\;x<0\end{array}\right.$┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉(8分)
(2)由方程f(x)=0有五个不相等的实数解,得y=f(x)的图象与x轴有五个不同的交点,┉┉┉(9分)
因为f(x)为奇函数,所以函数y=f(x)的图象关于原点对称,又f(0)=0,
所以f(x)=x2+mx+1(x>0)的图象与x轴正半轴有两个不同的交点,┉┉┉(10分)
即,方程x2+mx+1=0有两个不等正根,记两根分别为x1,x2┉┉┉┉┉┉(12分)
$⇒\left\{\begin{array}{l}△={m^2}-4>0\\{x_1}+{x_2}=-m>0\\{x_1}•{x_2}=1>0\end{array}\right.⇒m<-2$,┉┉┉┉┉┉┉┉┉┉┉┉(15分)
所以,所求实数m的取值范围是m<-2┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉(16分)
点评 本题考查函数的奇偶性的运用:求解析式,考查方程思想和函数思想转化,注意运用韦达定理,考查运算能力,属于中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | A={-1,0,1},B={0,1},f:A中的数平方 | B. | A={0,1},B={-1,0,1},f:A中的数开方 | ||
| C. | A=Z,B=Q,f:A中的数取倒数 | D. | A=R,B={正实数},f:A中的数取绝对值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20不是这个数列中的项 | B. | 只有第5项是20 | ||
| C. | 只有第9项是20 | D. | 这个数列第5项、第9项都是20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{5}$,0),($\sqrt{5}$,0) | B. | (0,-$\sqrt{5}$),(0,$\sqrt{5}$) | C. | (-$\sqrt{13}$,0),($\sqrt{13}$,0) | D. | (0,-$\sqrt{13}$),(0,$\sqrt{13}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
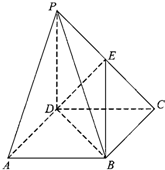 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com