
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
分析 点P(2,0)不在圆x2-2ax+a2+y2-4y=0外,则$\sqrt{(2-a)^{2}+{2}^{2}}$≤4,解出即可判断出结论.
解答 解:圆x2-2ax+a2+y2-4y=0配方化为:(x-a)2+(y-2)2=4,
若点P(2,0)不在圆x2-2ax+a2+y2-4y=0外,则$\sqrt{(2-a)^{2}+{2}^{2}}$≤4,解得$2-2\sqrt{3}$≤a≤2+2$\sqrt{3}$,
∴“a=2“是“点P(2,0)不在圆x2-2ax+a2+y2-4y=0外”的充分不必要条件.
故选:A.
点评 本题考查了点与圆的位置关系、两点之间的距离公式、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=60°,AC=CC1=2,BC=1,E,F分别是A1C1,BC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=60°,AC=CC1=2,BC=1,E,F分别是A1C1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
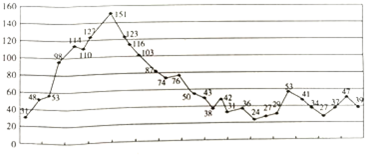
| 空气质量 指数类别 | 优 [0,35] | 良 (35,75] | 轻度污染 (75,115] | 中度污染 (115,150] | 重度污染 (150,250] | 严重污染 (250,500] | 合计 |
| 频数 | 30 | ||||||
| 频率 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
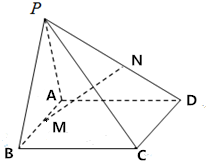 如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.
如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com