
分析 (1)求出函数的定义域,函数的导数,利用斜率求出a,即可.
(2)化简函数的导数,通过①当a≥0时,②当a<0时,分别求解函数的单调区间即可.
解答 解:(1)由题知f(x)的定义域为(0,+∞),且$f'(x)=\frac{{4a{x^2}+(a+4)x+1}}{x}$.
又∵f(x)的图象在$x=\frac{1}{4}$处的切线与直线4x+y=0平行,
∴$f'(\frac{1}{4})=-4$,即$4[4a×\frac{1}{16}+(a+4)×\frac{1}{4}+1]=-4$.解得a=-6.…(6分)
(2)$f'(x)=\frac{{4a{x^2}+(a+4)x+1}}{x}=\frac{(4x+1)(ax+1)}{x}$,由x>0,知$\frac{4x+1}{x}$>0.
①当a≥0时,对任意x>0,f'(x)>0,f(x)在(0,+∞)上单调递增.
②当a<0时,令f'(x)=0,解得$x=-\frac{1}{a}$,
当$0<x<-\frac{1}{a}$时,f'(x)>0,当$x>-\frac{1}{a}$时,f'(x)<0,
此时,f(x)的单调递增区间为$(0,-\frac{1}{a})$,递减区间为$(-\frac{1}{a},+∞)$.…(12分)
点评 本题考查函数的导数的综合应用,函数的单调性与极值,切线方程的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,5] | B. | [$\frac{3}{2}$,11] | C. | [$\frac{1}{5}$,$\frac{2}{3}$] | D. | [$\frac{1}{5}$,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -4 | C. | $\frac{2}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 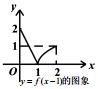 | B. | 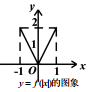 | C. | 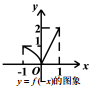 | D. | 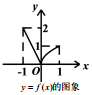 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
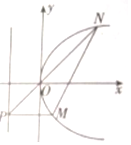 椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,过F2作x轴垂直的直线交椭圆C于A、B两点,△F1AB的面积为3,抛物线E:y2=2px(p>0)以椭圆C的右焦点F2为焦点.
椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,过F2作x轴垂直的直线交椭圆C于A、B两点,△F1AB的面积为3,抛物线E:y2=2px(p>0)以椭圆C的右焦点F2为焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com