
分析 (Ⅰ)求出f(x)的导数,求得切线的斜率和切点坐标,再由已知切线方程即可得到m;
(Ⅱ)求出导数,讨论m的范围,当m≤0时,当m>0时,令导数大于0,得增区间,令导数小于0,得减区间,从而求出函数的最大值即可;
(Ⅲ)设g(x)=lnx-mx+m,即有g(x)max<0在x>1恒成立.求出g(x)的导数,对m讨论,当m≤0时,当m>0时讨论①当$\frac{1}{m}$≤1即m≥1时,②当$\frac{1}{m}$>1即0<m<1时,通过单调性求得最大值,即可得到m的范围.
解答 解:(Ⅰ)∵m=2,∴f(x)=lnx-2x,x=1时f(1)=ln1-2=-2,
f′(x)=$\frac{1}{x}$-2,∴f′(1)=1-2=-1,
切线方程为:y+2=-(x-1)=-x+1,即x+y+1=0;
(Ⅱ)∵f′(x)=$\frac{1}{x}$-m,(x>0),
当m≤0时,f'(x)>0恒成立,
则单调递增区间为(0,+∞),无单调减区间;
故f(x)在[1,e]上单调递增,
fmax(x)=f(e)=lne-me=1-me,
当m>0时,由f′(x)>0得 0<x<$\frac{1}{m}$,
由f′(x)<0,得x>$\frac{1}{m}$,
∴f(x)在(0,$\frac{1}{m}$)递增,在($\frac{1}{m}$,+∞)递减,
①若0<$\frac{1}{m}$≤1,即m≥1时,fmax(x)=f(1)=-m,
②若1<$\frac{1}{m}$<e,即$\frac{1}{e}$<m<1时,fmax(x)=f($\frac{1}{m}$)=ln$\frac{1}{m}$-1=-lnm-1,
③若$\frac{1}{m}$≥e,即m≤$\frac{1}{e}$时,fmax(x)=f(e)=lne-me=1-me,
综上:当m≤$\frac{1}{e}$,fmax(x)=1-me,$\frac{1}{e}$<m<1时,fmax(x)=-lnm-1,
m≥1时,fmax(x)=f(1)=-m;
(Ⅲ)由f(x)+m≤0,可得lnx-mx+m≤0在x>0恒成立.
设g(x)=lnx-mx+m,即有g(x)max≤0在x>0恒成立.
由于g′(x)=$\frac{1}{x}$-m,
由(Ⅱ)知当m≤0时,g(x)在x>0上递增,
?x>0,g(x)无最大值,不合题意舍去;
当m>0时,g(x)在(0,$\frac{1}{m}$)递增,在($\frac{1}{m}$,+∞)递减,
g(x)max=g($\frac{1}{m}$)=-lnm+m-1=0,解得:m=1符合题意;
综上可得,m=1.
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,主要考查导数的几何意义和函数的单调性的运用,运用分类讨论的思想方法是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | S=1+2+3+…100,P=1+2+3+…100 | B. | S=1+2+3+…99,P=1+2+3+…100 | ||
| C. | S=1+2+3+…99,P=1+2+3+…99 | D. | S=1+2+3+…100,P=1+2+3+…99 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是抛物线形拱桥,当水面在时,拱顶离水面2m,水面宽4m,如果水位下降$\frac{5}{2}$m后(水深大于5m),水面宽度为( )
如图是抛物线形拱桥,当水面在时,拱顶离水面2m,水面宽4m,如果水位下降$\frac{5}{2}$m后(水深大于5m),水面宽度为( )| A. | 1m | B. | 6m | C. | $2\sqrt{5}$m | D. | 4m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
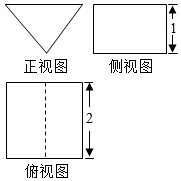 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com