
分析 (1)求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的最大值即可;
(2)求出g(x)关于直线x=$\frac{1}{2}$对称,只需证明:x1-x+(1-x)x≤$\sqrt{2}$在(0,$\frac{1}{2}$]恒成立,求出函数的导数,根据函数的单调性证明即可.
解答 (1)解:f′(x)=lnx+ln(1-x)+2,
令f′(x)=0,解得:x=$\frac{1}{2}$-$\sqrt{\frac{1}{4}-\frac{1}{{e}^{2}}}$(记为x0),
则f(x)在(0,x0)递减,在(x0,$\frac{1}{2}$]递增,
x→0+时,f′(x)→0,f(π)≤f($\frac{1}{2}$)=0,即xlnx-(1-x)ln(1-x)≤0,
∴f(x)在(0,$\frac{1}{2}$]上的最大值是0;
(2)证明:∵g(x)=x1-x+(1-x)x满足:g(x)=g(1-x),
∴g(x)关于直线x=$\frac{1}{2}$对称,
故只需证明:x1-x+(1-x)x≤$\sqrt{2}$在(0,$\frac{1}{2}$]恒成立,
而g′(x)=x1-x(-lnx+$\frac{1-x}{x}$)+(1-x)x[ln(1-x)-$\frac{x}{1-x}$],
而g($\frac{1}{2}$)=$\sqrt{2}$,只需证明g′(x)≥0,①在(0,$\frac{1}{2}$]恒成立,
而-xlnx+1-x>0,
即只需证明:$\frac{{(1-x)}^{1-x}}{{x}^{x}}$≥$\frac{-(1-x)ln(1-x)+x}{-xlnx+1-x}$②,
而由(1)可得0<x≤$\frac{1}{2}$时,(1-x)1-x≥xx,即$\frac{{(1-x)}^{1-x}}{{x}^{x}}$≥1③,
要使②式成立,只需证明$\frac{-(1-x)ln(1-x)+x}{-xlnx+1-x}$≤1在(0,$\frac{1}{2}$]上恒成立,
即只需φ(x)=xlnx-(1-x)ln(1-x)+2x-1≤0④,
由(1)得:xlnx-(1-x)ln(1-x)≤0,而2x-1≤0,
从而④式成立,
综合③④可知②式成立,
故①式得证,从而原不等式得证.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想、是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a?α,b?α,c⊥a,c⊥b 则c⊥α | B. | 若a⊥α,b⊥α 则a∥b | ||
| C. | 若a∥α,α∩β=b 则a∥b | D. | 若b?α,a∥b 则 a∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
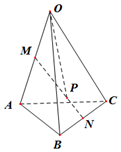 已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )| A. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
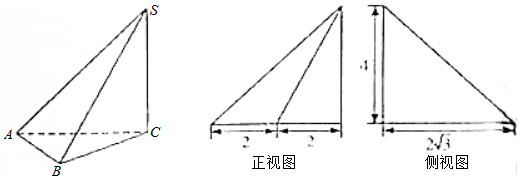
| A. | 32π | B. | $\frac{112π}{3}$ | C. | $\frac{28π}{3}$ | D. | $\frac{64}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 8 | C. | 4 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2) | C. | (2,5] | D. | [2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
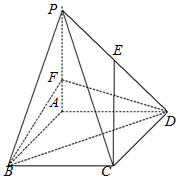 如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.
如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com